Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 12
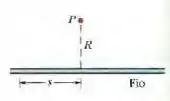
Na figura 29-43, o ponto está a uma distância de um fio retilíneo muito longo que conduz uma corrente. O campo magnético ao ponto P é a soma das contribuições de elementos de corrente ao longo de todo o fio. Determine a distância entre o ponto P e o elemento (a) que mais contribui para o campo e (b) responsável por da maior contribuição.
Passo 1
E aí, galera! 😁
Nesse problema temos um fio longo e nosso objetivo é determinar uma distancia de um ponto a uma distância em que mais contribui para o campo e outra distância que cointribui com da maior contribuição.
Tem ideia de como fazemos isso? 🤔
Tomando o eixo como horizontal e o eixo como vertical na figura 29-37, o vetor que liga um segmento do fio ao ponto P é dado por:
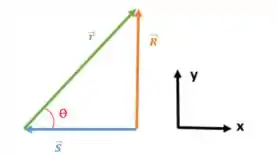
Como a direção do comprimento do fio retilíneo é o eixo :
Onde:
Assim:
Bora começar! 😉
Passo 2
A lei de Biot- Savart nos dá:
Assim, como e , temos
Como a variável aparece apenas no denominador, o elemento que mais contribui para o campo é o elemento situado em . Pois nesse caso diminuímos o valor do denominador, então o valor resultante é maior.
O valor de obtido fazendo na equação anterior, é:
Tranquilo até aqui? 😁
Passo 3
Assim a condição de que campo produzido seja responsável por da maior contribuição pode ser expressa através da equação:
Cortando alguns termos dos dois lados, temos:
Multiplicando cruzado:
Explicitando na equação anterior, obtemos:
E aí! Entendeu tudo? Responde Aí! 😎
Resposta
- Como a variável aparece apenas no denominador, o elemento que mais contribui para o campo é o elemento situado em ;
- .