Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 87
A configuração consiste em duas partículas puntiformes, uma tem carga e está no eixo em e a outra partícula tem carga e está em (Figura 23-26ª). Considerando que o potencial seja zero a grandes distâncias das partículas carregadas, mostre que o potencial também é zero em uma placa plana metálica de extensão infinita e uma partícula puntiforme localizada a uma distância da placa (Figura 23-36b). A partícula puntiforme tem uma carga igual a e a placa está aterrada. (O aterramento da placa obriga o seu potencial a ser igual a zero). Escolha a linha perpendicular à placa e que passa através da carga puntiforme como o eixo , e escolha a origem na superfície da placa, a mais próxima da partícula. (Estas escolhas colocam a partícula no eixo em ). Para a configuração , o potencial é zero em todos o spontos no semi espaço que estão muito afastados da partícula e em todos os pontos do plano – assim no caso da configuração . Um teorema denominado teorema da unicidade, implica que através do semiespaço a função potencial – e portanto, o campo elétrico – para as duas configurações são idênticos. Usando este resultado, obtenha o campo elétrico em cada ponto no plano na configuração . (O teorema da unicidade diz que na configuração o campo elétrico em cada ponto do plnao é o mesmo que na configuração .) Use este resultado para encontrar a densidade superficial de carga em cada ponto no plano condutor (na configuração )
Passo 1
Falaa galera! Baita enunciado, né? Gosto muito desse problema, pois ele trata de um dos conceitos mais bonitos da eletrostática: o método da imagem. Em eletrostática avançada, vemos que a resolução de uma equação (conhecida como equação da Laplace) irá nos fornecer o teorema da unicidade (citado no enunciado da questão). Basicamente, poderemos tratar uma carga localizada em de um plano infinito aterrado, como sendo uma carga em e outra carga em (o plano funciona como um espelho plano, por isso o nome “método das imagens”.
Passo 2
- Aqui, temos a seguinte configuração:
- Vamos usar o teorema da unicidade. O campo elétrico na configuração (A) é o mesmo que na configuração (B). Porém, o da configuração (A) é muito mais simples de ser calculado... veja que beleza :D
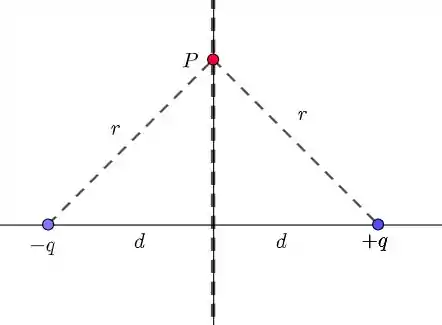
Veja que
Assim, todos os pontos no plano estarão sob potencial nulo. Para pontos muito distantes, temos (por definição).
Passo 3
Vamos então, calcular o campo elétrico da figura (A)
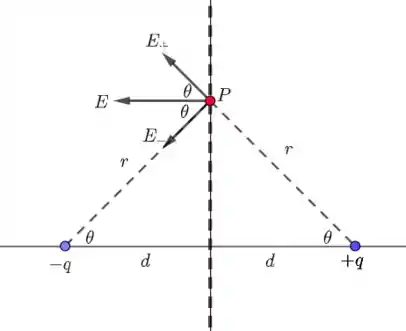
Temos
O campo resultante é:
A densidade de um plano é dada por
Resposta
- Ver acima.