Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.Problemas Adicionais - Ex. 90
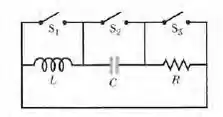
Considere o circuito da Figura 31-39. Com a chave fechada e as outras duas chaves abertas, a constante de tempo do circuito é . Com a chave fechada e as duas outras chaves abertas, a constante de tempo do circuito é . Com a chave fechada e as outras duas chaves abertas, o circuito oscila com um período . Mostre que .
Passo 1
Fala aí! tudo certinho? 😎
Nesse problema temos um circuito com três chaves , e . Nosso objetivo é mostrar que com a chave fechada e as outras duas chaves abertas, a constante de tempo do circuito é . Com a chave fechada e as duas outras chaves abertas, a constante de tempo do circuito é . Com a chave fechada e as outras duas chaves abertas, o circuito oscila com um período . Mostre que .
Pra isso vamos analisar o circuito em cada ocasião...
Veja só! 😉
Passo 2
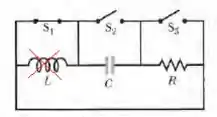
Quando a chave está fechada e as outras duas estão abertas, o indutor fica fora do circuito e o circuito resultante é um circuito , cuja a constante de tempo é
Tranquilo até aqui? 😁
Passo 3
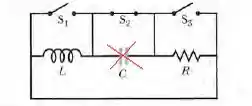
Quando a chave está fechada e as outras duas estão abertas, o capacitor fica fora do circuito e o circuito resultante é um , cuja constante de tempo é
Bacana, não é? 😬
Passo 4
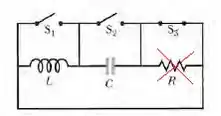
Quando a chave está fechada e as outras duasestão abertas, o resistor fica fora do circuito e o circuito resultante é um circuito , que oscila com um período . Fazendo e , obtemos:
E aí! o que achou? Responde Aí! 😉