Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 66

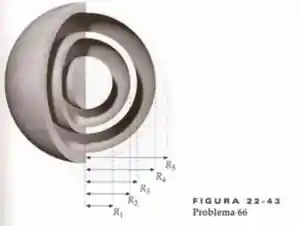
Considere a esfera metálica e as cascas esféricas concêntricas mostradas na Figura 22-43. Na parte mais interna está uma esfera sólida com raio R 1 . Uma casca esférica circunda a esfera, tendo raio interno R 2 e raio externo R 3 . A esfera e a casca estão circundadas por uma segunda casca esférica, que tem raio interno R 4 e raio externo R 5 . Todos os três objetos têm, inicialmente, arga resultante nula. Então, uma carga negativa - Q 0 é colocada na esfera interna e uma carga positiva + Q 0 é colocada na casca mais externa. (a) Depois de atingido o equilíbrio, qual será a direção e o sentido do campo elétrico entre a esfera interna e a casca intermediária? (b) Qual será a carga na superfície interna da casca intermediária? (c) Qual será a carga na superfície exterior da casca intermediária? (d) Qual será a carga na superfície interna da casca mais externa? (e) Qual será a carga na superfície exterior da casca mais externa? (f) Faça um gráfico de E como função de r para todos os valores de r .

Passo 1

Fala minha gente... probleminha bastante grande, né? Mas se acalme, vamos fazer tudo passo a passo, beleza?

Passo 2

Vamos primeiro entender o que está acontecendo. A gente tem uma série de esferas uma dentro da outra, correto? A primeira é uma esfera condutora, e depois temos cascas esféricas de espessuras não desprezíveis. Damos uma carga - Q 0 na esfera interna e + Q 0 na casca mais externa. Pela indução que a esfera faz sobre a casca de raio R 2 , então:

  • A casca de raio R 2 terá carga + Q 0 .

    • Para manter a neutralidade da casca interna, então:

  • A casca de raio R 3 terá carga - Q 0 .

    • Essa casca irá induzir sobre a casca de raio R 4 uma carga + Q 0 . Então:

  • A casca de raio R 4 terá carga + Q 0 .

    • Para manter a casca mais externa com carga + Q 0 a casca de raio R 5 terá carga igual a zero.

  • A casca de raio R 5 estará neutra.

    • Vamos agora responder aos itens.

    Passo 3

  1. Notemos que o campo elétrico aponta para o centro da esfera, pois a carga da esfera interna é negativa (campo de aproximação) e da casca de raio R 2 é positiva (campo de afastamento).
  2. Como vimos, + Q 0 .
  3. Como vimos, - Q 0 .
  4. Como vimos, + Q 0 .
  5. Como vimos, a casca estará neutra.
  6. Vamos aplicar a lei de Gauss nessas regiões:
  • Para 0 < r < R 1 : como a esfera é sólida e condutora, então E = 0 nessa região.
  • Para R 1 < r < R 2 . A carga interna será + Q 0 . Assim, aplicando Gauss,

    • E 4 π r 2 = Q 0 ⟹ E = Q 0 4 π r 2

  • Para R 2 < R < R 3 , o campo será nulo, pois estaremos no interior de um condutor carregado.
  • Para R 3 < R < R 4 , a carga total será igual a + Q 0 . Sendo assim, temos

    • E = Q 0 4 π r 2

  • Para R 4 < R < R 5 , E = 0 pois estamos no interior de um condutor.
  • Para R > R 5 , então a carga total é igual a zero... logo o campo em toda a região externa é nulo!!

    • Veja um gráfico esquemático.

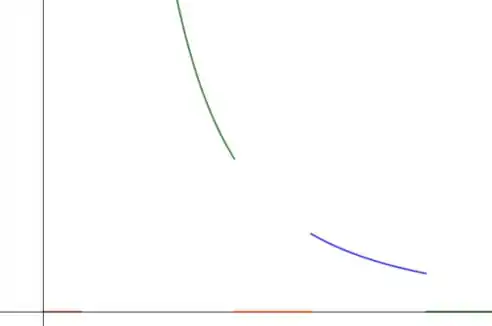
    Resposta

    Ei, a resposta está no passo a passo :)

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    A Fig. 23-38 é uma seção de uma barra condutora de raio R 1 = 1,30m m e comprimento L = 11,00m no interior de uma casca coaxial, de paredes finas, de raio R 2 = 10,0 R 1 e mesmo comprimento L . A carg
    Um cilindro maciço, longo, não condutor, com 4,0c m de raio, possui uma densidade volumétrica de cargas não uniforme ρ que é função da distância radial r a partir do eixo do cilindro: ρ=Ar 2 . Se A=2,
    Um elétron é arremessado na direção do centro de uma placa metálica que possui uma densidade superficial de cargas de - 2,0 × 10 - 6C / m 2 . Se a energia cinética inicial do elétron é 1,60 ×10 - 17J
    Duas grandes placas de metal com 1,0m 2 de área são mantidas paralelas a 5,0c m de distância e possuem cargas de mesmo valor absoluto e sinais opostos nas superfícies internas. Se o módulo E do campo
    Na Fig. 23-45, uma pequena esfera não condutora de massa m=1,0m g e carga q=2,0 ×10 - 8 C (distribuída uniformemente em todo o volume) está pendurada em um fio não condutor que faz um ângulo θ=30 º º