Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.8 - Ex. 41
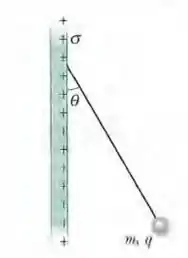
Na Fig. 23-45, uma pequena esfera não condutora de massa e carga (distribuída uniformemente em todo o volume) está pendurada em um fio não condutor que faz um ângulo com uma placa vertical, não condutora, uniformemente
carregada (vista de perfil). Considerando a força gravitacional a que a esfera está submetida e supondo que a placa possui uma grande extensão, calcule a densidade superficial de cargas da placa.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui queremos a densidade superficial de carga dado que a esfera é submetida a uma força elétrica que a deixa em equilíbrio.
Primeiro, bora trabalhar com o diagrama de corpo livre da partícula de massa :
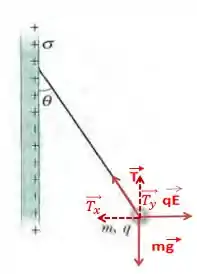
Onde é a tensão no fio, é a força eletrostática que a placa exerce sobre a esfera, é a força peso da esfera, e são as componentes da tensão no fio.
Passo 2
Como ela está em equilíbrio na horizontal:
Na vertical também temos equilíbrio. Então:
Dividindo a primeira equação pela segunda, a gente tem que:
Podemos cortae e substituir pela tangente:
Passo 3
Como , que é o campo elétrico de uma placa infinita (pode ser também uma lâmina infinita, mas o problema chama de placa), então:
Onde é a densidade de cargas da placa.
Isolando , temos:
Substituindo os valores que temos:
Fazendo essas contas: