Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 94
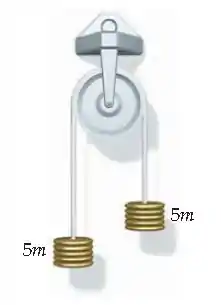
Considere a máquina de Atwood ideal da Figura 4-65. Quando arruelas são transferidas do lado esquerda para o lado direito, o lado direito desce em . Encontre
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre do sistema está exposto abaixo:
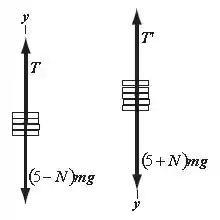
Aplicando a segunda lei de Newton, temos:
Temos também que:
Como , temos:
Usando a equação da posição para aceleração constante, temos que:
Como a velocidade inicial é nula, temos que:
Substituindo os valores, temos que:
Logo será:
Resposta
Exercícios de Livros Relacionados
Um bloco de massa m 1 = 3,70k g sobre um plano sem atrito inclinado, de ângulo θ = 30,0 ° , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um
44. Um pintor de paredes usa o arranjo de uma cadeira e uma polia mostrado na FIGURA P7.44 para se erguer pelo lado externo de uma residência. A massa do pintor é de 70k g , e a da cadeira, 10k g . Co
41. O livro de física de 1,0k g da FIGURA P7.41 está ligado por um barbante a uma caneca de café de 500g . Dá-se um pequeno empurrão no livro para cima e ele é liberado com uma velocidade de 3,0m / s
40. Uma caixa de 4,0k g , sobre uma rampa sem atrito e inclinada em 35°, está ligada a um peso de 20k g , suspenso, através de um barbante de massa desprezível que passa por uma polia, também sem mass
42. O bonde mostrado na FIGURA P7.42 desce uma colina de 200m de altura. Além dos freios, o bonde pode controlar sua velocidade puxando um contrapeso de 1.800k g que sobe simultaneamente pelo outro la