Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 73
Um projétil é lançado com a rapidez a um ângulo acima da horizontal. Encontre uma expressão para a altura máxima que ele atinge, acima do ponto de lançamento, em função de e (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Ele quer a expressão para altura máxima do projetil em função de e .
A gente tem essa situação:
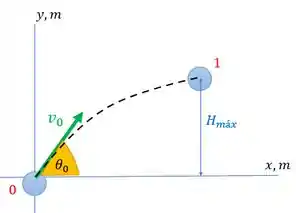
Percebe que a gente tem um lançamento de projetil, né? Nesse movimento, o que acontece verticalmente independe do que acontece horizontalmente. No movimento vertical temos um movimento de aceleração constante. E no horizontal temos velocidade constante.
Se a gente quer a altura máxima, queremos uma informação do movimento vertical, certo? Então a gente só vai olhar para esse movimento.
Para começar, podemos encontrar a velocidade inicial vertical . Ela é a projeção de em . E por isso tem essa expressão:
Outra coisa muito importante é a gente lembrar que no ponto mais alto da sua trajetória, a velocidade vertical do objeto é nula. Então no ponto momento onde ele está no ponto mais alto, temos:
Então a ideia aqui é a gente usar essas informações para avaliar o movimento vertical que acontece e achar a altura máxima do projétil. Vamos ver como!
Passo 2
Agora vamos refletir. O movimento vertical tem aceleração constante, que é a gravidade
Ela é negativa pois sempre aponta para baixo e o nosso é positivo para cima.
Se temos aceleração constante, valem as equações para o movimento com aceleração contante, certo?
Agora vamos pensar nos nossos dados. Temos a velocidade em dois pontos da trajetória: no ínicio e na altura máxima. Temos a aceleração. E queremos o deslocamento entre esses dois pontos, certo? Isso dá a altura que o projetil subiu.
E não temos nada falando sobre tempo decorrido também. Essas são dicas para gente usar a equação de Torricelli, que relaciona o deslocamento do projétil com a sua velocidade final e inicial. Ela tem essa carinha ao relacionar a velocidade do ponto 0 com o ponto 1:
Passo 3
Para usar essa bonita para o nosso caso, vamos substituir nossos dados. Temos que
E queremos descobrir . Substituido essas coisas:
Isolando quem a gente quer: