Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.Problemas - Ex. 81
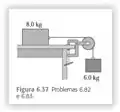
Considere o sistema indicado da Figura abaixo. A corda e a polia possuem massas desprezíveis, e a polia não possui atrito. A corda e a polia possuem massas desprezíveis, e a polia não tem atrito. Inicialmente, o bloco de 6,00 kg desloca-se verticalmente para baixo e o bloco de 8,00 kg desloca-se para a direita, ambos com velocidade de 0,900 m/s. Os blocos entram em repouso após percorrerem 2,00 m. Use o teorema do trabalho-energia para calcular o coeficiente de atrito cinético entre o bloco de 8,0 kg e o topo da mesa.
Passo 1
Faaala ae, beleza?? Probleminha de energia pra gente, bora lá!!
Primeira coisa é analisar as forças que estão agindo sobre os dois blocos:
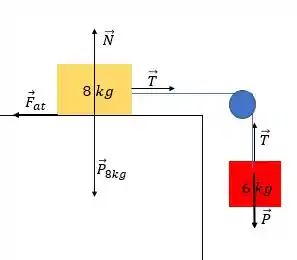
Onde é a força de atrito, é a tração no cabo da polia, é o peso do bloco de , é a força normal devido ao contato do bloco de com o solo e é a força peso do bloco de . Beleza??
E, agora, podemos ver que as forças normal e peso do bloco de vão se anular, certo? Isso porque não teremos movimento na vertical nesse bloco. Então, não vamos nos preocupar com elas.
Além disso, a dica aqui é considerar os dois blocos como um só! Sabe porquê? Porque, como as trações nos blocos são iguais, ao considerarmos os dois juntos, elas se cancelam também!
Dessa forma, sobram quais forças? A de atrito e a peso do bloco de .
Passo 2
Agora, vamos pensar no seguinte: o que diz o teorema trabalho-energia?? Bom, ele diz que o trabalho realizado pela força resultante é igual à variação da energia cinética:
Opa, então, precisamos achar a variação da energia cinética e o trabalho da força resultante.
Passo 3
O enunciado diz que, inicialmente, temos ambos os blocos com velocidade e, depois de , eles entram em repouso. Então, nossa variação da energia cinética será:
Lembrando que estamos considerando como se fosse apenas um bloco, então :
Passo 4
E o trabalho das forças?? Bom, a força de atrito vai realizar um trabalho e o peso do bloco de também, mas em direções contrárias! Lembrando que o trabalho de uma força é calculado por:
Onde é o ângulo entre o deslocamento e a força. No caso da força de atrito, ela aponta para a esquerda e o bloco se move para a direita, então . No caso da força peso, ambos apontam na mesma direção! Logo, .
A força de atrito realiza o trabalho:
Lembrando que e , onde é o coeficiente de atrito cinético e é a força normal do bloco de .
Como vimos na imagem do passo 1, e se cancelam, logo, possuem o mesmo valor:
Dessa forma, o trabalho da força de atrito fica:
E a força peso??
Ela realiza um trabalho de:
Como , e :
Passo 5
Beleza!! Agora, podemos usar o teorema trabalho-energia:
Substituindo o que calculamos:
Agora, vamos isolar :
Beleza?? Acabou! 😊