Considere um sistema de três partículas de mesma massa , ocupando os vértices de um triangulo equilátero de lado . (a) Calcule a força gravitacional que atua sobre cada partícula, em módulo, direção e sentido. (b) Mostre que as três partículas mantêm essa configuração triangular descrevendo órbitas circulares em torno do CM do sistema com velocidade angular . Calcule o valor de . Este caso particular solúvel do problema de três corpos foi considerado por Laplace.
Passo 1
Nessa aí a gente vai usar um pouquinho a ajuda dos vetores, então primeiro bora estabelecer um sistema de eixos pra botar essas partículas.
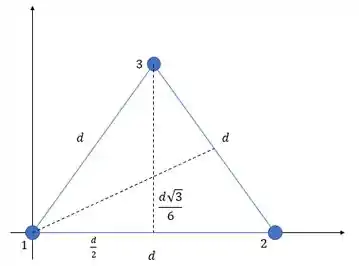
Com a ajuda desse gráfico, vamos calcular as forças que atuam nas partículas. Então, primeiro vamos olhar pra partícula .
A soma das duas é a força que atua na partícula!
E o módulo dessa força é:
E qual é a direção dessa força? Ela faz um ângulo com o eixo que vale:
Que é exatamente a direção do centro de massa!!!
Passo 2
Para as outras duas, vamos seguir o mesmo padrão. Primeiro para a partícula :
E para a partícula :
Passo 3
A força gravitacional é a única que atua no corpo, então ela vai ser igual à resultante centrípeta!
O raio de giração é a distância até o centro de massa, igual a .