Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 69
Um satélite em uma órbita circular de raio r tem período T. Em uma órbita próxima de raio , onde , outro satélite apresenta período levemente diferente, .
- Demonstre que
- Dois satélites terrestres estão em órbitas paralelas de raios e . Um dia eles passam um pelo outro, a 1 km de distância ao longo de uma linha radialmente externa à Terra. Quanto tempo transcorrerá até que eles se encontrem novamente a 1 km de distância?
Passo 1
Temos um problema de um corpo (no caso um satélite) orbitando um outro corpo de massa muito maior (no caso um planeta). Nesse caso, o satélite irá descrever uma órbita circular (ou elíptica, mas o enunciado deixa claro que a órbita é circular!). A velocidade do satélite pode ser calculada! Para tal, basta repararmos que a força gravitacional é uma componente centrípeta, como mostra a figura abaixo.
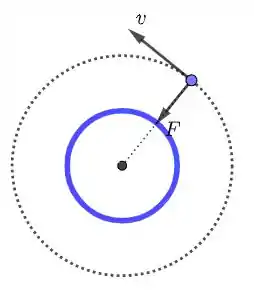
Assim, temos que
Note que a velocidade é constante durante o movimento circular. Sendo assim, temos que:
Vamos usar essa última equação para resolver a questão!!
Passo 2
- Notemos que:
- Note que as órbitas são muito próximas... assim, podemos usar o resultado anterior.
E
Porém, vamos usar a seguinte aproximação:
Essa aproximação é válida apenas quando (ou seja, é muito menor do que ). Assim, temos:
Como . Logo, podemos usar a aproximação citada acima; além disso, usando , temos:
que é o que queríamos provar!!
Passo 3
Temos que:
Para o outro satélite, temos (note que ). Logo, aplicando o resultado do item a:
Logo,
Assim, a velocidade angular do primeiro satélite é:
A velocidade angular do segundo satélite é:
Assim, podemos escrever as equações do movimento circular para esses satélites:
Os satélites vão se encontrar novamente quando:
Vamos usar novamente a aproximação dada no Passo 2:
Portanto, segue que o tempo necessário será:
onde dividimos o resultado por 86.400 para obter o tempo em dias!
Resposta
Irá demorar dias.