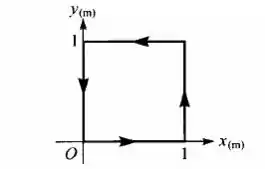
Uma partícula se move no plano xy sob a ação da força F 1 = 10 ( yi ^ - xj ^ ) , onde | F 1 | é medido em N, e x e y em m. a) Calcule o trabalho realizado por F 1 ao longo do quadrado indicado na figura. b) Faça o mesmo para F 2 = 10 ( yi ^ + xj ^ ) . c) O que você pode concluir a partir de a) e b) sobre o caráter conservativo ou não de F 1 e F 2 ? d) Se uma das duas forças parece ser conservativa, procure obter a energia potencial U associada, tal que F = -grad U.

a ) W =- 20J b )W = 0J c )F 1n ã op o d es e rc o n s e r v a t i v a .F 2p o d es e r ã d )U x , y = - 10 x y

Enunciado

Para calcular o trabalho vamos escrever os vetores deslocamento de cada parte do trajeto. Vamos começar na origem e seguir as setas enumerando elas de 1 a 4.

No caso genérico, temos isso aqui ó

Vamos agora aplicar para cada parte da trajetória

Tendo em mente essas continhas abaixo vamos conseguir fazer tudo de boa, chega mais!

Vamos aplicar distributivas para resolver a parte de dentro da integral, nesse caso por exemplo temos

Aqui a ideia é a mesma, só vamos mudar a fórmula da força, tranquilo? Fica assim

Se o trabalho for de uma força conservativa, ao retornamos ao mesmo ponto inicial, independente da trajetória, o trabalho resultante será nulo. Assim a gente conclui que a força 1 não é conservativa, tranquilo? Já a força 2 atende a esse requisito, mas não quer dizer que ela é necessariamente conservativa. Caso ela seja a gente vai encontrar uma funçãozinha potencial, show?

Como

Integrando os dois lados em temos

Vamos derivar nossa função encontrada com respeito a y

Agora igualamos à componente correspondente da força. Fica assim,

Nossa função potencial fica então , se escolhermos uma delas em que temos