Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.8 - Ex. 40
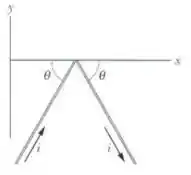
O fio dobrado da Fig. 28-45 está submetido a um campo magnético uniforme. Cada trecho retilíneo tem de comprimento e faz um ângulo com o eixo . O fio é percorrido por uma corrente de . Qual é a força que o campo magnético exerce sobre o fio, em termos dos vetores unitários, se o campo magnético é (a) ; (b) ?
Passo 1
E aí, galerinha! 😉
Aqui temos um fio dobrado submetido a um campo magnético e é percorrido por uma corrente, e é pedido a força que o campo magnético exerce sobre o fio.
Lembra como fazemos isso? 👀
Para calcular a força entre um campo magnético e um fio percorrido por uma corrente podemos utilizar a equação
Onde é a corrente e o comprimento do fio.
Veja só! 😉
Passo 2
(a) Por simetria, concluímos que a componente da força que o campo magnético exerce sobre o fio é zero. De acordo com a regra da mão direita, um campo na direção produz nas duas partes do fio uma componente da força que aponta na direção e cujo módulo é
com os valores , , e
Assim, a força total que o campo exerce sobre o fio é .
Tranquilo até aqui? 😁
Passo 3
(b) Nesse caso, a força que o campo exerce sobre o lado esquerdo do fio aponta no sentido e a força que o campo exerce sobre o lado direito do fio aponta no sentido .
Como, por simetria, as duas forças são iguais, a força total é 0.
E aí! entendeu tudo? Responde Aí! 😁
Resposta
(a)
(b) zero