Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.9 - Ex. 49
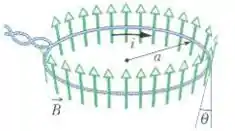
A Fig. 28-48 mostra um anel circular de fio com um raio , submetido a um campo magnético divergente de simetria radial. O campo magnético em todos os pontos do anel tem o mesmo módulo , é perpendicular ao anel e faz um ângulo com a normal ao plano do anel. A influência dos fios de alimentação da espira pode ser desprezada. Determine o módulo da força que o campo exerce sobre a espira se a corrente na espira é
Passo 1
E aí, pessoal! 😉
Nesse problema temos um anel circular de fio com um raio , submetido a um campo magnético divergente de simetria radial. O campo magnético em todos os pontos do anel tem o mesmo módulo , é perpendicular ao anel e faz um ângulo com a normal ao plano do anel.
A partir daí queremos determinar o módulo da força que o campo exerce sobre a espira se a corrente na espira é
Tem ideia de como fazemos isso? 🤔
Bem, vamos considerar um segmento infinitesimal desse anel, . O campo magnético é perpendicular ao segmento, portanto temos que . Dessa forma, podemos calcular as componentes do campo:
Saca só! 😬
Passo 2
Por simetria, a força em que aponta para o centro do anel é zero.
Basta, pensar que todos os pontos do anel vão estar tendo a mesma componente que aponta diretamente para o centro, somando todos eles têm que se anular.
Agora a componente em :
Essa integral é o perímetro de um círculo, portanto:
Se , , e , então...
E aí! o que achou? Responde Aí! 😁
