Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.8 - Ex. 44
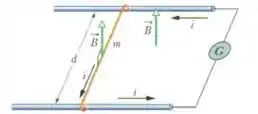
Na Fig. 28-46, um fio metálico de massa pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância . O conjunto está em uma região onde existe um campo magnético uniforme de módulo . No instante , um gerador é ligado aos trilhos e produz uma corrente constante no fio e nos trilhos (mesmo quando o fio está se movendo). No instante , determine (a) a velocidade escalar do fio; (b) o sentido do movimento do fio (para a esquerda ou para a direita).
Passo 1
Fala aí! tudo certinho? 😁
Bem, temos esse fio metálico de massa que tem tamanho e está em uma região onde existe um campo magnético . Em um determinado instante um gerador é ligado e passa a corrente pelo fio.
E nosso objetivo é determinar a velocidade do fio no instante .
Parece complicado? 🤔
Para determinar a velocidade do fio no instante , vamos primeiramente escrever a seguinte relação cinemática:
Sendo a variação de velocidade, a aceleração e a variação do tempo
Podemos usar a segunda lei de Newton com a fórmula para a força magnética, para calcular a aceleração:
Em que é a corrente elétrica, é a distância, é o campo magnético e a massa
Veja só! 😉
Passo 2
Portanto, se substituirmos a segunda equação na primeira, vamos obter
Agora substituímos os valores dados no enunciado, temos , , , e .
(b) Usando a regra da mão direita o sentido é para a esquerda.
E aí! entendeu tudo? Responde Aí! 😬
Resposta
(a)
(b) O sentido é para a esquerda.