Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.8 - Ex. 46

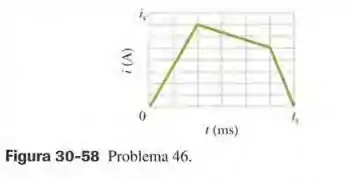
A corrente i em um indutor de 4,6   H varia com o tempo t de acordo com o gráfico da Fig. 30-58, onde a escala do eixo vertical é definida por i s = 8,0   A . A escala do eixo horizontal é definida por t s = 6,0   m s . O indutor tem uma resistência de 12   Ω . Determine o módulo da força eletromotriz induzida ε (a) para 0 < t < 2   m s ; (b) para 2   m s < t < 5   m s ; (c) para 5   m s < t < 6   m s . (Ignore o comportamento nos extremos dos intervalos.)

Passo 1

O problema fornece o gráfico da corrente num indutor em função do tempo e pede para acharmos o módulo da fem induzida em diversos intervalos de tempo.

Sabemos que

ε = - L d i d t

Note que nos intervalos considerados, o gráfico da corrente como função do tempo é formado por retas, de modo que

d i d t = Δ i Δ t

Além disso, como estamos interessados apenas no módulo da fem:

ε = L Δ i Δ t

Passo 2

No item (a), para 0 < t < 2   m s

ε = ( 4,6   H ) ( 7,0 A - 0 ) 2,0 × 10 - 3 s = 1.6 × 10 4 V = 16 k V

Passo 3

Já no item (b), para 2 < t < 5   m s

ε = ( 4,6   H ) ( 5 , 0 A - 7 , 0 A ) ( 5,0 - 2,0 ) × 10 - 3 s = 3 , 1 × 10 3 V = 3,1 k V

Passo 4

Por fim, o item (c), para 5 < t < 6   m s

ε = ( 4,6   H ) ( 0 A - 5 , 0 A ) ( 6 , 0 - 5 , 0 ) × 10 - 3 s = 2,3 × 10 4 V = 23   k V

Resposta

ε = 16   k W

ε = 3,1 k W

ε = 23   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois solenóides toroidais são enrolados sobre um mesmo núcleo de modo que o campo magnético de um passa através das espiras do oturo. O toróide 1 possui 700 espiras, enquanto o toróide 2 possui 400 es
Um solenoide reto e longo possui N espiras, a seção reta com área A e comprimento l . Mostre que a indutância deste solenoide é dada pela equação L = μ 0 A N 2 l Suponha que o campo magnético seja uni
De acordo com a equação 30.5 , 1 H = 1 W b / A , e, de acordo com a equação 30.41 H = 1 Ω ⋅ s . Mostre que essas duas definições são equivalentes.
Quando a corrente em um solenoide toroidal está variando com uma taxa igual a 0.026 A s , o módulo da fem é igual a 12,6 m V . Quando a corrente é igual a 1.4 A , o fluxo magnético médio através de ca
Duas bobinas são enroladas sobre um mesmo núcleo cilíndrico, como as bobinas do Exemplo 30.1. Quando a corrente na primeira bobina diminui com uma taxa de - 0.242A / s , a fem induzida na segunda bobi