Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.7 - Ex. 43

Dois fios longos iguais, de raio , são paralelos e conduzem correntes iguais em sentidos opostos. A distância entre os eixos centrais dos fios é . Despreze o fluxo no interior dos fios, mas considere o fluxo na região entre os fios. Qual é a indutância dos fios por unidade de comprimento?

Passo 1

O problema diz que dois fios muito longos (vamos aproximar por fios infinitos) conduzem uma corrente em sentidos contrários. Vamos posicionar o fio com corrente para baixo no eixo e o outro fio (corrente para cima) com seu eixo na reta . O raio dos fios é denotado por .

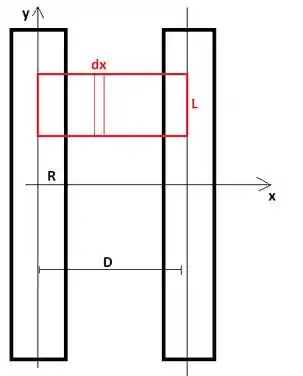
Queremos o fluxo por unidade de comprimento na região entre os fios . Para isso, vamos considerar a região retangular (em vermelho) com base e altura . O fluxo nessa região:

representa a soma do campo devido aos dois fios. Como o fio da esquerda tem corrente para baixo e o da direita para cima, os campos gerados entre os fios terão mesmo sentido (para fora da figura, isto é, na direção positiva). Desta forma, os campos se somam:

Por fim, uma última simplificação que podemos fazer: note que há uma simetria com relação à reta . O fluxo de até é igual ao fluxo de até (pense bem nisso antes de aceitar viu?). Assim,

Passo 2

Note que entre e , o campo magnético criado pelo fio 1 (fio da esquerda com corrente para baixo) é diferente para (dentro do fio) e para (fora do fio). Dentro do fio, o campo magnético cresce linearmente com :

Já fora do fio, temos à expressão clássica:

Essas expressões foram todas deduzidas e trabalhadas no capítulo 29. Já para o fio 2 (da direita com corrente para cima):

Assim, o fluxo será

Mas antes de calcularmos essas integrais, lembre-se que devemos desconsiderar o fluxo dentro dos fios. Assim, a primeira integral deve ser desconsiderada e na última, o limite inferior de integração será (não ). Assim,

Fazendo as integrações:

Desta forma, o fluxo por unidade de comprimento entre os fios será:

Passo 3

Sabemos que a indutância é definida por

Assim, a indutância por unidade de comprimento dos fios será

Substituindo e , chegamos em

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bobina retangular com N espiras compactas é colocada nas proximidades de um fio retilíneo longo, como mostra a figura 30-66. Qual é a indutância mútua M da combinação fio-bobina para N = 100 ,a =

Duas bobinas são mantidas fixas no espaço. Quando a corrente na bobina 1 é zero e a corrente na bobina 2 aumenta à taxa de 15,0A / s , a força eletromotriz na bobina 1 é 25,0m V . (a) Qual é a indutân

As duas bobinas da figura 30-68 têm indutâncias L 1 e L 2 quando estão muito afastadas. A indutância mútua é M . (a) Mostre que a combinação que aparece na figura pode ser substituida por uma indutânc

A bobina 1 tem L 1 = 25m H e N 1 = 100 espiras. A bobina 2 tem L 2 = 40m H e N 2 = 200 espiras. As bobinas são mantidas fixas no espaço; a indutância múta é 3,0m H . Uma corrente de 6,0m A na bobina 1

Dois solenoides fazem parte do circuito de ignição de um automóvel. Quando a corrente em um dos solenoides diminui de 6,0A para zero em 2,5m s , uma força eletromotriz de 30k V é induzida no outro sol