Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.8 - Ex. 58

Uma criança que pesa 267   N desce em um escorrega de 6 ,   1   m que faz um ângulo de 20 ° com a horizontal. O coeficiente de atrito cinético entre o escorrega e a criança é 0,10 . (a) Qual é a energia transformada em energia térmica? (b) Se a criança começa a descida no alto do escorrega com uma velocidade de 0,457   m / s , qual é sua velocidade ao chegar ao chão?

Passo 1

Oi, galerinha! Tudo bom? Vamos começar desenhando o que está acontecendo para entender melhor:

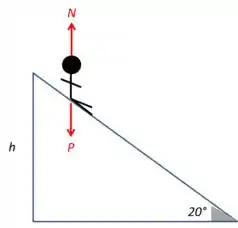
Fazendo o equilíbrio de forças que agem no eixo perpendicular ao plano do escorregador, encontramos:

F N - P . c o s θ = 0

F N = P . c o s θ

O aumento de energia térmica é dado por:

∆ E t = f . d

Como f = μ k . F N ,

∆ E t = μ k . F N . d

∆ E t = μ k . P . c o s θ . d

∆ E t = 0,10 . 267   N . 6,1 m . c o s ⁡ ( 20 ° )

∆ E t = 1,5.10 2 J

Passo 2

b) Agora vamos usar a lei de conservação da energia!

Temos que a variação de energia potencial é dada por:

∆ U = m g h

Como a força peso é dada por P = m g , e pela figura temos que a altura h é dada por h = - d s e n θ , temos que

∆ U = P . ( - d s e n θ )

Substituindo os valores,

∆ U = 267 N . - 6,1   m . s e n ( 20 ° )

∆ U = - 5,6.10 2 J

Já a energia cinética inicial igual a:

K i = 1 2 m . v i 2

K i = 1 2 267   N 9,81 m s 2 . ( 0,457   m / s ² )

K i = 2,8   J

Passo 3

Assim, de acordo com a lei de conservação de energia, temos:

K f = K i - ∆ U - ∆ E t

K f = ( 2,8   J ) - ( - 5,6.10 2 J ) - ( 1,5.10 ² J )

K f = 4,1   . 10 2 J

Logo, a velocidade final é dada por:

v f = 2 K f m

v f = 2 . ( 4,1.10 2   J ) 276 N 9,81   m / s ²

v f = 2 . ( 4,1.10 ²   J ) 267 N 9,81   m / s ²

v f = 5,5   m / s

Resposta

a)   ∆ E t = 1,5.10 2 J

b)   v f = 5,5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força horizontal constante faz um baú de 50k g subir 6,0 m em um plano inclinado de 30 ° com velocidade constante. O coeficiente de atrito cinético entre o baú e o plano inclinado é 0,20 . Qual é
Um escorrega de parquinho tem a forma de um arco de circunferência com 12m de raio . A altura do escorrega é h=4,0m e o chão é tangente à circunferência (Fig. 8-68). Uma criança de 25k g escorrega do
Uma haste rígida de massa desprezível e comprimentoL possui uma bola de massam presa a uma das extremidades (Fig. 8-66). A outra extremidade está presa a um eixo de tal forma que a bola pode se mover
Um projétil de 9,40k g é lançado verticalmente para cima. O arrasto do ar diminui a energia mecânica do sistema projétil- Terra de 68,0k J durante a subida do projétil. Que altura a mais o projétil te
Um nadador se desloca na água a uma velocidade média de 0,22m / s . A força de arrasto média é 110N . Que potência média o nadador está desenvolvendo?