Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 133
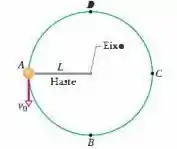
Uma haste rígida de massa desprezível e comprimento possui uma bola de massa presa a uma das extremidades (Fig. 8-66). A outra extremidade está presa a um eixo de tal forma que a bola pode se mover em uma circunferência vertical. Primeiro, suponha que não existe atrito no eixo. A bola é lançada para baixo a partir da posição horizontal com velocidade e para exatamente no ponto . (a) Escreva uma expressão para em termos de , e . (b) Qual é a tensão da haste quando a bola passa pelo ponto? ( c) Coloca se um pouco de areia no eixo para aumentar o atrito. Depois disso, a bola chega apenas ao ponto quando é lançada a partir de com a mesma velocidade de antes. Qual é o decréscimo de energia mecânica durante o movimento? (d) Qual é o decréscimo de energia mecânica quando a bola finalmente entra em repouso no ponto após várias oscilações?
Passo 1
Então galera , a primeira coisa que devemos fazer é definir as condições iniciais do problema. Tomando o ponto como referência para a energia potencial, a energia mecânica total nos pontos , e é dada por :
Em que . A boa para resolvermos esse problema é usar a lei de conservação da energia, segundo a qual
A condição de que nos dá que :
Passo 2
Para calcular a tensão da haste quando a bola passa pelo ponto B, calculamos primeiro a velocidade no ponto . Fazendo obtemos que :
Reparem que quando a bola está nessa posição, a aceleração centrípeta aponta para cima, na mesma direção da tensão. Assim, de acordo com a Segunda Lei de Newton,
O que nos dá .
De boa , pessoal? Bora continuar então que ainda não acabou
Passo 3
Bom galera , como a diferença de altura entre os pontos e é , nós sabemos que o decréscimo de energia mecânica é dado por :
Passo 4
Utilizando umraciocínio análogo ao do item anterior , como a diferença de altura entre os pontos e é a energia mecânica que foi perdida pode ser calculada pela relação :
Resposta
Respectivamente :
Tranquilo galera??? Bora resolver mais questões então!!!!!!