8. || Uma curva de auto-estrada com raio de 500 m foi projetada para
o tráfego a 90 km/h. Qual é o ângulo correto de inclinação lateral
da pista?
Passo 1
Eai, se liga nesse enunciado. Ele ta pedindo o ângulo de inclinação da pista e não da nenhum coeficiente de atrito, ou seja, toda a força centripeta vai surgir da componente horizontal da normal.
Ele ta dando a velocidade e o raio da circunferência, então podemos calcular qual vai ser a força centripeta.
Sabemos que a força centripeta é igual a massa vezes a aceleração centripeta (2ª Lei de Newton). E sabemos que a aceleração centripeta é igual a velocidade ao quadrado dividido pelo raio, assim:
Então a força cetripeta fica:
Vamos converter a velocidade para metros por segundo, só dividir por :
Agora sim, vamos substituir:
Calculando isso ai:
Passo 2
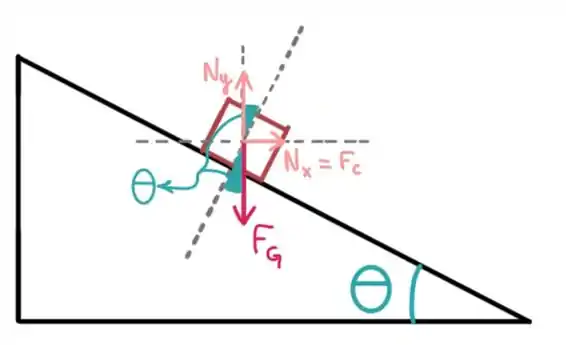
Vamos fazer um diagrama de corpo livre do carro pra gente não se perder com essas forças e com os ângulos:
Só temos essas duas forças no nosso carro. Então a componente da normal em deve ser igual ao peso e a componente da normal em deve ser igual a força centripeta. Assim:
Show, vamos montar a equação para o eixo :
Para o eixo :
Vamos fazer também as contas da decomposição da normal:
e
Vamos substituir nas equações dos eixos ali em cima:
e
Vamos dividir uma equação pela outra, desse jeito a gente some com a normal e com a massa:
Seno sobre cosseno é igual a tangente. CDa pra cortar a normal e cortar a massa.
Calculando essa angulo em uma calculadora: