Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Exercício - Ex. 45
Em um dado ponto de um escaneamento cilíndrico horizontal, a velocididade da água é igual a 2,50m/s e a pressão manométrica é igual a . Calculce a pressão manométrica em um segundo ponto do encanamento sabendo que o diâmetro do cano no segundo ponto é igual ao dobro do diâmetro do primeiro.
Passo 1
Fala aí pessoal, tudo bem? Bora fazer essa questão juntos?
Temos um caso em que precisamos encontrar a pressão manométrica num segundo ponto do encanamento, em que o diâmetro é duas vezes maior que no ponto anterior, a situação é essa aqui:
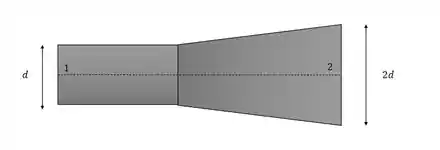
Imagina que temos esse cano circular e no segundo ponto o diâmetro do tubo é o dobro do primeiro ponto, e os pontos estão na mesma altura.
Pra gente calcular essa pressão vamos usar duas equações, a equação da continuidade e a equação de bernoulli, beleza?
A relação das áreas vai ajudar a gente na hora de analisar a equação da continuidade e a relação das alturas na equação de bernoulli, então vamos nessa.
Passo 2
Aplicando a equação da continuidade temos o seguinte, a vazão nos dois pontos é a mesma.
E aqui vai entrar o lance do diâmetro, se liga aí temos que cada área circular é dada por:
Sendo assim a relação das velocidades fica:
E cortando os semelhantes:
E se liga aí, nós temos essa velocidade inicial:
Logo:
Com essa velocidade poderemos aplicar a equação de Bernoulli.
Passo 3
Assim, podemos aplicar a equação de bernoulli nos pontos:
Logo, a pressão manométrica no ponto 2 é de
A pressão do manômetro é mais alta no segundo ponto, porque a velocidade da água é menor lá.