Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 11

Um medidor tipo Venturi é inserido numa tabulação inclinada de raio R , onde se escoa um fluido de densidade ρ . O estreitamento tem raio r e os ramos do manômetro são inseridos em pontos de alturas z 1 e z 2 ; o líquido manométrico tem densidade ρ f . Calcule a vazão Q do fluido na tubulação em função destes dados e do desnível h entre os dois ramos do manômetro.

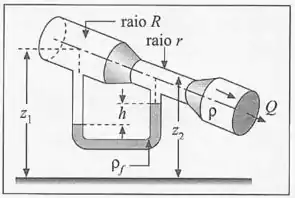
Passo 1

Vamos começar montando a equação de Bernoulli para os pontos que correspondem às alturas z 1 e z 2 :

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p 2 + ρ g z 2 + 1 2 ρ v 2 2

Ok, isso não nos leva muito longe. Vamos tentar usar a equação da continuidade para relacionar v 1 e v 2 :

A 1 v 1 = A 2 v 2

π R 2 v 1 = π r 2 v 2

v 2 = R 2 r 2 v 1

E agora vamos elevar os dois lados ao quadrado para substituir na equação de Bernoulli:

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p 2 + ρ g z 2 + 1 2 ρ R 4 r 2 v 1 2

Reorganizando um pouco:

p 1 - p 2 = ρ g z 2 - z 1 + 1 2 ρ v 1 2 R 4 r 4 - 1

Beleza, eliminamos uma variável.

Passo 2

Agora vamos pensar na diferença de pressão entre os dois pontos. Como ela se relaciona com o desnível h do líquido manométrico?

Vamos considerar dois pontos A e B na mesma altura dentro do tubo:

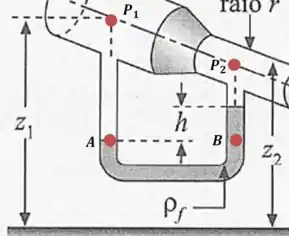
As pressões em A e B devem ser iguais. Vamos escrever expressões para cada uma delas:

p A = p 1 + ρ g h + ρ g z 1 - z 2

p B = ρ f g h + p 2

E então:

p 1 + ρ g h + ρ g z 1 - z 2 = ρ f g h + p 2

p 1 - p 2 = ρ f - ρ g h + ρ g z 2 - z 1

E substituindo isso na equação de Bernoulli:

ρ f - ρ g h + ρ g z 2 - z 1 = ρ g z 2 - z 1 + 1 2 ρ v 1 2 R 4 r 4 - 1

Podemos cortar mais duas variáveis:

ρ f - ρ g h = 1 2 ρ v 1 2 R 4 r 4 - 1

E então a velocidade v 1 é:

v 1 = 2 ρ F - ρ g h ρ R 4 r 4 - 1

Passo 3

Nosso objetivo final é encontrar a vazão volumétrica Q na extremidade do tubo.

No ponto v 1 , podemos calcular:

Q 1 = π R 2 v 1

Mas pela equação da continuidade, Q 1 = Q , então:

Q = π R 2 2 ρ F - ρ g h ρ R 4 r 4 - 1

Resposta

A vazão é Q = π R 2 2 ρ F - ρ g h ρ R 4 r 4 - 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura ilustra uma variante do tubo de Pitot, empregada para medir a velocidade v de escoamento de um fluido de densidade ρ . Calcule v em função do desnível h entre dois ramos do manômetro e da den
Um sifão é estabelecido aspirando o líquido do reservatório (de densidade ρ ) através do tubo recurvado A B C e fazendo-o jorrar em C , com velocidade de escoamento v . (a) Calcule v em função dos par
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d
Um tomado é um redemoinho de ar muito veloz. Por que a pressão no centro é sempre muito menor que na periferia? Como essa condição é responsável pelo poder de destruição de um tomado?