Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 12

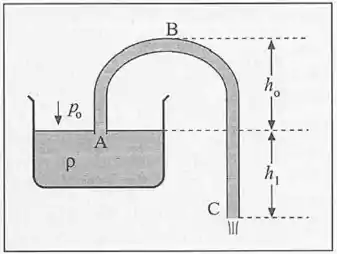
Um sifão é estabelecido aspirando o líquido do reservatório (de densidade ρ ) através do tubo recurvado A B C e fazendo-o jorrar em C , com velocidade de escoamento v . (a) Calcule v em função dos parâmetros da figura P7. (b) Calcule a pressão nos pontos A e B . (c) Qual é o valor máximo de h 0 para o qual o sifão funciona?

Passo 1

(a) Vamos começar aplicando a equação de Bernoulli para dois pontos.

O ponto P 1 na superfície do reservatório, sob pressão p 0 e velocidade praticamente nula.

O ponto P 2 na saída do tubo, também sob pressão p 0 (porque está em contato com a atmosfera), e com velocidade v . Então:

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p 2 + ρ g z 2 + 1 2 ρ v 2 2

p 0 + ρ g z 1 + 1 2 ρ 0 = p 0 + ρ g z 2 + 1 2 ρ v 2

ρ g z 1 = ρ g z 2 + 1 2 ρ v 2

A diferença de altura dos pontos é dada na figura, pois z 1 - z 2 = h 1 , então:

v = 2 g h 1

Passo 2

(b) Agora queremos encontrar a pressão no ponto A (na entrada do tubo). Vamos usar a equação de Bernoulli mais uma vez.

Podemos comparar o ponto A ao nosso ponto P 1 na superfície do reservatório:

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p A + ρ g z A + 1 2 ρ v A 2

Dessa vez temos z 1 = z A :

p 1 + 1 2 ρ v 1 2 = p A + 1 2 ρ v A 2

Como vimos antes, a velocidade em P 1 é nula e p 1 = p 0 , então:

p 0 = p A + 1 2 ρ v A 2

A velocidade v A é medida logo na entrada do tubo.

Como o tubo tem uma área transversal constante, a velocidade é constante ao longo dele. Então podemos aproveitar o valor que calculamos antes:

v A = 2 g h 1

p 0 = p A + ρ g h 1

p A = p 0 - ρ g h 1

Passo 3

Para o ponto B , a única diferença é que z 1 ≠ z B :

p 1 + ρ g z 1 + 1 2 ρ v 1 2 = p B + ρ g z B + 1 2 ρ v B 2

Mais uma vez temos p 1 = p 0 , v 1 = 0 e v B = 2 g h 1 :

p 0 + ρ g z 1 = p B + ρ g z B + ρ g h 1

E z B - z 1 = h 0 , então:

p 0 = p B + ρ g h 0 + ρ g h 1

p B = p 0 - ρ g h 0 + h 1

Passo 4

(c) Para que o sifão funcione, o fluido tem que ser capaz de subir pelo menos até o ponto B , certo? Se ele chegar nesse ponto, a partir dali ele só precisa ser puxado pela gravidade.

Então no caso limite de funcionamento do sifão, a pressão no ponto B vai ser igual a zero. Vamos usar a fórmula que acabamos de demonstrar:

p B = p 0 - ρ g h 0 + h 1

Quando p B = 0 temos h 0 = h 0 , m á x :

0 = p 0 - ρ g h 0 , m á x + h 1

h 0 , m á x = p 0 ρ g - h 1

Resposta

(a) v = 2 g h 1 .

(b) p A = p 0 - ρ g h 1 e p B = p 0 - ρ g h 0 + h 1 .

(c) O valor máximo é h 0 = p 0 ρ g - h 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na vitrine de uma loja, uma bola de tênis de mesa flutua no ar empurrada por um jato de ar vindo da saída do cano de um aspirador de pó. A bola oscila um pouco, porém sempre permanece próxima do centr
Em um dado ponto de um encanamento horizontal, a velocidade da água é igual a 2,50 m/s e a pressão manométrica é igual a 1,80 X 10 4 Pa. Calcule a pressão manométrica em um segundo ponto do encanament
Um pequeno orifício circular com diâmetro igual a 6,00 mm é cortado na superfície lateral de um grande tanque de água, a uma profundidade de 14,0 m abaixo da superfície. O topo do tanque está aberto p
Um sistema de irrigação de um campo de golfe descarrega água de um cano horizontal à taxa de 7 .200 c m 3 / s . Em um ponto do cano em que o raio é 4,0 cm, a pressão absoluta da água é 2,40 X 10 5 Pa.
Artéria obstruída. O sangue viscoso está escoando por uma artéria parcialmente obstruída pelo colesterol. Um cirurgião deseja remover uma quantidade suficiente do colesterol para dobrar a vazão de san