Dados três vetores não-coplanares e , mostre que é o volume do paralelepipdo formado pelos três vetores
Passo 1
Nossa representação fica assim, olha só:
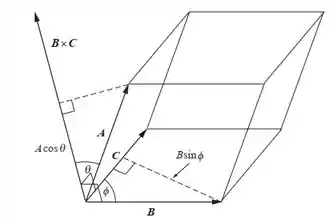
Pode parecer bem assustador no primeiro momento, mas calma!
Passo 2
O modulo de é o seguinte:
Mas,
área da base do paralelograma formado por e .
Logo, o modulo do produto vetorial é a área da base!!
Passo 3
Agora vamos olhar para
Isto é:
E olharmos para , estamos pegando a altura com relação a “base” formada por e . Portanto, representa a altura!
Assim,
Resposta
Ei, a resposta está no passo a passo :)