Verdedeiro ou falso:

1. Se dois vetores têm sentidos opostos, seu produto vetorial deve ser zero.
2. A magnitude do produto vetorial de dois vetores é mínima quando os vetores são perpendiculares.
3. O conhecimento da magnitude do produto vetorial de dois vetores não-nulos, além das magnitudes individuais dos vetores, permite a determinação unívoca do ângulo entre eles.

a) Vamos avaliar. Se dois vetores estão em uma mesma direção, mas sentidos opostos, o ângulo entre esses vetores é , e aí

Então essa é verdadeira!

b) Se os vetores são perpendiculares, o ângulo entre eles é , e então na expressão do produto vetorial o seno vai assumir o maior valor possível que é .

O que faz com que o valor do resutado do produto vetorial seja máximo e não mínimo. Logo, essa é falsa.

c) Vamos entender o que ele falou. Ele diz se a gente conhece o módulo do resultado do produto vetorial entre dois vetores, e também o módulo desses dois vetores separadamente, ou seja, se conhecemos

Ele diz que podemos encontrar o ângulo entre eles. Mas cuidado, ao dizer “determinação unívoca do ângulo”, ele quer dizer que vamos com certeza encontrar apenas um ângulo.

Agora vamos analisar, se a gente tiver esses dados que ele falou e jogá-los na nossa equação do passo 1

A gente pode isolar para achar o valor dele, repara

Ele diz que a partir dessa equação, achamos somente um valor para . Mas, isso não é verdade. Por que? Esse argumento do arcoseno é positivo porque só temos módulos ali, né?

Então, esse ângulo vai estar onde o seno é positivo. Só que o seno é positivo em dois quadrantes do círculo trigonométrico, então teremos dois ângulos com mesmo valor de seno que satisfazem essa equação.

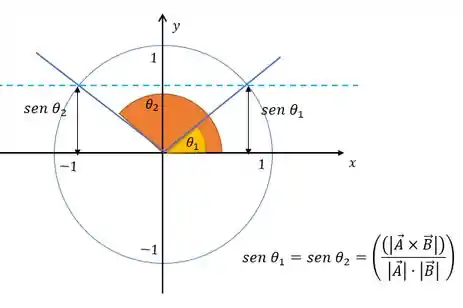
Portanto, o ângulo não está determinado unicamente. E essa afirmativa é falsa.