Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 105

Uma demonstração de sala de aula popular, mas perigosa, é segurar uma bola de beisebol cerca de uma polegada diretamente acima de uma bola de basquete que você segura alguns pés acima de um piso duro e largar as duas bolas simultaneamente. As duas bolas colidirão logo após a bola de basquete repicar no piso; a bola de beisebol será, então, lançada até o teto, enquanto a bola de basquete parará brucamente. (a) Supondo que a colisão da bola de basquete seja elástica, qual é a relação entre as velocidades das bolas justo antes delas colidirem? (b) Supondo que a colisão entre as duas bolas seja elástica, use o resultado da parte (a) e conservação da quantidade de movimento e da energia para mostrar que, se a bola de basquete é três vezes mais pesada do que a de beisebol, a velocidade final da bola de basquete será zero. (Esta é, aproximadamente, a verdadeira razão de massas, o que torna a demonstração tão dramática.) (c) Se a rapidez da bola de beisebol é v justo antes da colisão, qual é sua rapidez logo após a colisão?

Passo 1

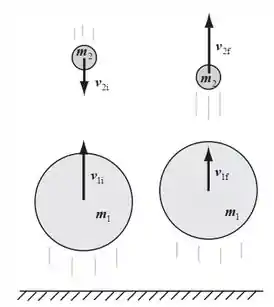
  1. Como as duas bolas estão em queda livre, e as duas caem pela mesma quantidade de tempo, as duas vão ter a mesma velocidade no momento em que a primeira (bola de basquete) chega ao chão e quica. Depois que a bola de basquete quica (elasticamente), as velocidades vão ter a mesma velocidade, mas estarão na direção oposta. Portanto, as velocidades das bolas serão iguais em módulo, mas em direções opostas.

Passo 2

b e c) Conservação da quantidade de movimento, adotando o sentido positivo para cima:

m 1 v 1 i - m 2 v 2 i = m 1 v 1 f + m 2 v 2 f

3 m 2 v 1 i - m 2 v 2 i = 3 m 2 v 1 f + m 2 v 2 f

3 v 1 i - v 2 i = 3 v 1 f + v 2 f

3 v - v = 3 v 1 f + v 2 f

3 v 1 f + v 2 f = 2 v   ( * )  

Coeficiente de restituição (colisão elástica):

e = v a f a s t a m e n t o v a p r o x i m a ç ã o = 1

v 2 f - v 1 f = v 1 i + v 2 i = 2 v

v 2 f - v 1 f = 2 v   ( * * )

Subtraindo a segunda equação da segunda, vamos obter:

3 v 1 f + v 2 f - v 2 f - v 1 f = 0

4 v 1 f = 0

v 1 f = 0

v 2 f = 2 v

Resposta

  1. A mesma velocidade v , mas no sentido oposto.
  2. v 1 f = 0 , v 2 f = 2 v .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois blocos estão livres para deslizar ao longo da pista de madeira sem atrito mostrada na Figura P8.19. O bloco de massa m 1=5,00k g é solto da posição mostrada, a uma altura h=5,00m acima da parte p
Dois discos de shuffleboard de massas iguais, um laranja e outro amarelo, estão envolvidos em uma colisão oblíqua elástica. O disco amarelo está inicialmente em repouso e é atingido pelo disco laranja
Uma bola de bilhar movendo-se a 5,00m / s colide com outra parada com a mesma massa. Após a colisão, a primeira bola se move a 4,33m / s a um ângulo de 30,0 ° em relação à linha original de movimento.
Conforme mostra a Figura P8.20, uma bala de massa m e de velocidade escalar v passa completamente pelo pêndulo de massa M . A bala surge com uma velocidade dev / 2 . O pêndulo é suspenso por uma haste
Uma bola de tênis de massa m t é mantida exatamente acima de uma bola de basquete de massa m b , como mostrado na Figura P8.22. Com seus centros verticalmente alinhados, ambas são liberadas do repouso