Demonstre o resultado de Galileu enunciado à pg. 53, mostrando que, para uma dada velocidade v0, um projétil pode atingir o mesmo alcance A para dois ângulos de elevação diferentes, e , contanto que A não ultrapasse o alcance máximo . Calcule em função em função de e .

Quando chega questão de demonstrar : eita... pulei sem querer, kkkk. HOJE NÃO! Tou aqui pra te ajudar. Vem comigo!

Então, nesse caso aqui a gente pode analisar a fórmula do alcance de modo bastante simples.

Como sabemos que

Se gente pensar em 2 ângulos que vão nos dar o mesmo seno, teremos o mesmo alcance A, sim ou não? Bom, que valores eu coloco ali no espacinho do seno que vão me dar de volta uma resposta igual? Bora ver o ciclo trigonométrico

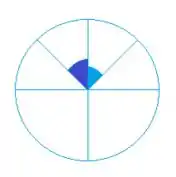
Na reta vertical temos os senos e na horizontal os cosenos, se a gente observar esses ângulos azul claro e escuro batem justamente no mesmo ponto da reta vertical, ou seja, tem o mesmo seno!!! Ótimo, e que ângulos são esses? Se a gente reparar são simétricos ao , então vamos escrever eles assim

Como na nossa fórmula do começo estamos considerando fica assim

Ou seja, alcances iguais pra ângulos diferentes!! Matamos.

Para calcular nosso ângulo usaremos a fórmula inicial, substituindo por , fica assim

Usando a fórmula de soma de ângulos obtemos