Uma carreta de carregando uma plataforma vertical para lançamento de foguetes se desloca para a direita, a uma velocidade constante de ao longo de uma pista horizontal. Essa plataforma lança um foguete de verticalmente de baixo para cima, com velocidade inicial de em relação à carreta.

a) Que altura o foguete atingirá?

b) Onde, em relação à carreta, o foguete aterrissará?

c) Que distância a carreta percorre enquanto o foguete está no ar?

d) Do ponto de vista de um observador em repouso no solo, a que ângulo, em relação à horizontal, o foguete se desloca assim que deixa a carreta?

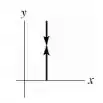
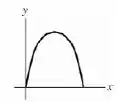
2) Desenhe a trajetória do foguete do ponto de vista de um observador i) parado na carreta e ii) parado no solo.

A altura máxima é atingida quando a velocidade vertical é igual a zero. Vou usar essa formula aqui:

E colocar para determinar a altura máxima:

Show?

Na direção horizontal, tanto o foguete quanto a carreta possuem a mesma velocidade, então ele aterrissará na carreta! Isso mesmo! Enquanto o foguete sobe e desce, ele também se movimenta para o lado.

A carreta segue seu movimento horizontal, então o foguete vai aterrissar na carreta.

Bacana, não é?

Precisamos determinar o tempo de voo. Para isso vamos usar a equação para a velocidade:

Admitindo que o foguete volte com a mesma velocidade de subida, porém com o sinal trocado, podemos achar o tempo de voo:

Agora a distância percorrida pode ser achada pela equação de movimento horizontal:

Tranquilo até aqui?

O ângulo é determinado pela tangente da razão das componentes iniciais:

Estamos quase lá!

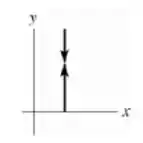Por fim, o problema pede os gráficos. Para um observador na carreta, o foguete sobe e desce verticalmente para cima. A representação gráfica é:

53,1 ° . O gráfico fica assim:

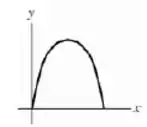
E aí! o que achou? Responde Aí!