Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 1

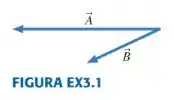
Desenhe os vetores da FIGURA EX3.1 sobre uma folha de papel. Depois determine

  1. A → + B → e
  2. A → - B →

Passo 1

  1. A → + B →

    2. Para determinar o vetor soma vamos seguir essas etapas:

    1. Desenhe o vetor   A → ;
    2. Desenho o vetor   B → com a cauda na pontinha do vetor   A → ;
    3. Desenhe uma seta que começa na calda de   A → e termina na pontinha de   B → . Esse é o vetor soma.

    Passo 2

    Então vamos lá seguir os passos:

    Primeiro vamos redesenhar a figura de modo que a cauda de   B → esteja na pontinha de   A → , desse jeito aqui:

    Nossos passos 1 e 2 estão prontos, agora temos que fazer uma seta ligando a calda de   A → com a pontinha de   B → .

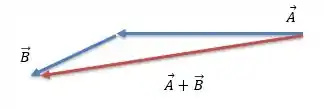
    Prontinho, o vetor em vinho é o nosso vetor soma.

    Passo 3

  2. A → - B →

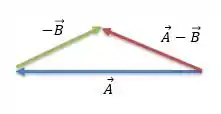
IHH, a gente sabe os passos para fazer uma soma, agora ele está pedindo uma subtração. Pronto, ferrou? Claroo que não.

A gente pode reescrever essa subtração como uma soma, saca só:

A → + ( - B → )

Viu? Agora só precisamos achar quem é o vetor - B → e depois seguir os mesmos passos que fizemos anteriormente.

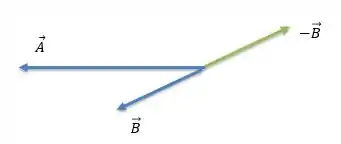
O sinal de menos ou mais em um vetor indica o sentido do vetor. Esse sinal de menos no vetor - B → quer dizer justamente que o vetor está no sentido contrário. Então, o vetor - B → é o vetor   B → mas com sentido contrário.

Passo 2

Agora que sabemos quem é o vetor - B → vamos seguir as regrinhas:

Primeiro vamos desenhar o vetor   A → e o vetor - B → com a calda na pontinha do vetor   A → :

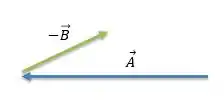
Agora vamos fazer a seta, ligando a calda do vetor   A → com a pontinha do vetor - B → :

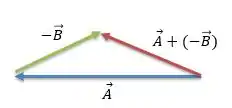
Prontinho, o vetor em vinho é o nosso vetor   A → - B → .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sim ou não: Cada uma das seguintes quantidades é um vetor? ForçaTemperaturao volume da água em uma lataas classificações de um programa de TVa altura de um edifícioa velocidade de um carro esportivoa
12. Mostre que, para u = c 1 c 2 , tem-se, ∆ P θ u∆ J z u ≥ 1 2 ℏ c 1 2 - c 2 2s e n2 θ - c 1 * c 2 + c 2 * c 1 cos ⁡ 2 θ e que o segundo membro é da ordem de ℏ .
Supondo um sistema de coordenadas com orientação da mão direita, ache a direção e o sentido do eixo Oz na a) Figura 1.13a, b) Figura 1.13b
Escreva cada vetor indicado na Figura 1.25 em termos dos vetores unitários i ^ e j ^ .
Para os vetores indicados na Figura 1.25, a) ache o módulo, a direção e o sentido do produto vetorial A → × B → ; b) ache o módulo, a direção e o sentido do produto vetorial B → × A →