Enunciado
Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 1.Exercícios - Ex. 40
Escreva cada vetor indicado na Figura 1.25 em termos dos vetores unitários e .
Passo 1
Oieee pessoal, tudo bom?
Para resolver essa questão precisamos analisar os vetores dispostos na Figura 1.25 para escrevê-los em termos dos componentes unitários.
Um vetor unitário é um vetor que possui módulo igual a 1, sem unidade, possuído o objetivo de apresentar uma direção e sentido no espaço. Eles nos auxiliam em cálculos de componentes de vetores. No plano x-y os vetores unitários são representados por e , onde é definido que o vetor unitário aponta no sentido positivo do eixo e o vetor unitário aponta no sentido positivo do eixo .
Um vetor pode ser representado pelos vetores unitários de acordo com a expressão abaixo, onde e são um valor numérico que representa o tamanho do vetor na direção e respectivamente.
Passo 2
Agora, vamos fazer os cálculos das componentes para os vetores da Figura 1.25.
Temos dois vetores: e . Ambos estão com sua origem localizada no nosso plano de coordenadas .
O vetor A possui apenas uma componente horizontal, perceba que ele não está inclinado em relação ao eixo como está o vetor B. Diante disso, conseguimos concluir que o vetor A possui apenas a componente . Além disso, ele aponta no sentido negativo do eixo , ou seja, teremos um sinal negativo na componente i.
Então, o vetor A é representado por:
Diante disso, precisamos calcular o valor de .
A Figura 1.25 indica o módulo de . Como ele possui apenas a componente , o valor do módulo corresponde ao nosso valor .
Então, a representação do vetor A em componentes fica:
Passo 3
Ao contrário do vetor A, o vetor B possui uma inclinação em relação ao eixo de 37 graus.
Ok! Então, de imediato sabemos que esse vetor possui tanto uma componente quanto uma componente . Ou seja, o vetor B é representado por:
Agora, resta saber seus valores. Para tal iremos utilizar o ângulo entre e o eixo e funções trigonométricas como cosseno e seno.
Traçamos um triângulo retângulo, onde a hipotenusa é o nosso vetor B e os catetos são as componentes, como na figura abaixo.
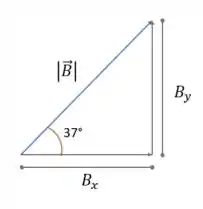
Para calcular a componente em :
Considerando :
Para calcular a componente em :
Considerando :
Portanto, a representação do vetor B em vetores unitários fica:
Resposta