Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.7 - Ex. 38

O deslocamento d → 1 está no plano y z , faz um ângulo de 63,0 ° com o semieixo y positivo, tem uma componente z positiva e tem um módulo de 4,50   m . O deslocamento d → 2 está no plano x z , faz um ângulo de 30,0 ° com o semieixo x positivo, tem uma componente z   positiva e tem um módulo de 1,40   m . Determine (a) d → 1 ⋅ d → 2 ; (b) d → 1 × d → 2 e (c) o ângulo entre d → 1   e   d → 2 .

Passo 1

Para visualizar melhor a situação vamos fazer um esboço, primeiro do plano yz:

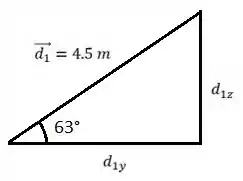
Agora do plano xz:

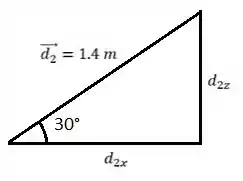
Vamos calcular, em termos dos vetores unitários, as componentes d 1 z , d 1 y , d 2 x e d 2 z :

d 1 z = ( 4,5   m ) ( c o s   63 ° ) ≃ ( 2,04 m )   j ^

d 1 y = ( 4,5   m ) ( s e n   63 ° ) ≃ ( 4,01 m )   k ^

d 2 x = ( 1,4 m ) ( c o s   30 ° ) ≃ ( 1,21 m )   i ^

d 2 z = ( 1,4   m ) ( s e n   30 ° ) ≃ ( 0,70 m )   k ^

Agora que já temos as componentes vamos calcular d → 1 e d → 2 :

d → 1 = 2,04   m j ^ + 4,01   m k ^

d → 2 = 1,21   m i ^ + 0,70   m k ^

Passo 2

O produto escalar d → 1   e   d → 2 pode ser obtido através da relação:

d → 1   .   d → 2 = 0 i ^   + 2,04 j ^ +   4,01 k ^ ⋅ 1,21 i ^ +   0 j ^ + 0,70 k ^

d → 1   .   d → 2 = ( 0 i ^ *   1,21 i ) ^ + 2,04 j ^ * 0 j ^ + (   4,01 k ^ * 0,70 k ^ )

d → 1   .   d → 2 = 4,01 k ^ ⋅ 0,70 k ^ =   2,81   m 2

Passo 3

O produto vetorial d → 1   e   d → 2 pode ser obtido através do determinante da matriz:

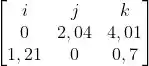
d → 1 × d → 2 = ( 0,7 * 2,04 ) i ^ + ( 1,21 * 4,01 ) j ^ + 0 k ^ - ( 2,04 * 1,21 ) k ^ - 0 i ^ - 0 j ^

d → 1 × d → 2 = ( 1,43   i ^ +   4,86 j ^ -   2,48 k ^ )

Passo 4

Os módulos d → 1   e   d → 2 são:

d → 1 = 2,04 m 2 + 4,01 m 2 =   4.50   m

    d → 2 = 1,21 m 2 + 0,70 m 2 =   1,40   m

Dessa forma , podemos obter o ângulo entre os dois vetores através da relação:

c o s   θ = d 1 → ⋅ d 2 → d 1 d 2

θ = c o s - 1   (   2,81   m 2 ( 4,50 m ) ( 1,40 m ) ) = 63,5 °

Resposta

(a) d → 1   .   d → 2 =   2,81   m 2

(b) d → 1 × d → 2 = ( 1,43   i ^ +   4,86 j ^ -   2,48 k ^ )

(c) θ = 63,5 °

De boa , galera???

Continuem resolvendo questões com a gente , adoramos ter vocês por aqui

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que A → • B → pode ser interpretado como o produto do módulo de A → vezes o componente de B → em relação a A → , ou o módulo
Ache o ângulo entre cada par de vetores: A → = - 2,0i ^ + 6,0j ^ e B → = 2,0i ^ - 3,0j ^ ;
Qual é o ângulo entre um vetor força F → e o torque τ → gerado por F → ?
Sejam dois vetores não-nulos, A → e B → . Seu produto vetorial possui magnitude máxima se A → e B → :São paralelosSão perpendicularesSão antiparalelosFormam um ângulo de 45 ° entre si
Verdedeiro ou falso:Se dois vetores têm sentidos opostos, seu produto vetorial deve ser zero.A magnitude do produto vetorial de dois vetores é mínima quando os vetores são perpendiculares.O conhecimen