Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 7.Exercícios e Problemas - Ex. 2

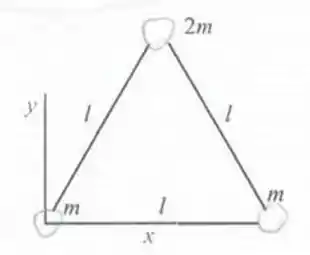
Determine a posição do centro de massa do sistema visto na Figura 7.12.

Passo 1

Salve pessoas, tudo certo? Vamos lá! Primeiro, vamos entender que dividiremos em coordenadas x e coordenadas y . E o melhor: Usaremos a mesma formula para os dois! Que delícia hein? Então sem perder tempo!

Passo 2

Para as coordenadas x , temos:

x m = 1 M t o t a l m 1 ⋅ p o s 1 + m 2 ⋅ p o s 2

Aplicando para o caso:

x m = 1 2 m m ⋅ 0 + m ⋅ l = l 2

Passo 3

Para as coordenadas y , temos:

x y = 1 4 m 2 m ⋅ 0 + 2 m ⋅ h = 1 2 ⋅ h

Mas o que é o “h”? É a altura do triângulo! Calcularemos usando o teorema de Pitágoras!

l 2 = l 2 2 + h 2

l 2 - l 2 4 = h 2

h = l 2 - l 2 4

Logo,

h = 3 2 l

h = 0.866 l

Voltando para a equação,

y m = 1 2 ⋅ h

y m = 1 2 ⋅ 0.866 l

y m = 0.433 l

Resposta

x m = l 2

y m = 0.433 l

Resposta

A d = 948.6   m e t r o s

B θ = 121.8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está
Exploradores da floresta encontram um monumento antigo na forma de um grande triângulo isósceles, como mostrado na Figura P8.37. O monumento é feito de dezenas de milhares de pequenos blocos de pedra
Romeu ( 77,0k g ) entretém Julieta ( 55,0k g ) tocando sua guitarra na parte traseira de seu barco que está em repouso em água parada, 2,70m afastado de Julieta, que está na parte da frente do barco.
7.4P A figura 7.14 mostra um reservatório cilíndrico cujas paredes têm espessura e densidade uniformes. O reservatório em massa m r e contém uma massa m a de água. Determine a posição do centro de mas