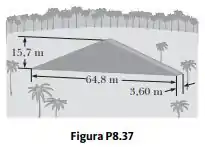
Exploradores da floresta encontram um monumento antigo na forma de um grande triângulo isósceles, como mostrado na Figura P8.37. O monumento é feito de dezenas de milhares de pequenos blocos de pedra de densidade . O monumento tem de altura e de largura em sua base, com espessura de ao longo dele. Antes de o monumento ser construído muitos anos atrás, todos os blocos de pedra foram colocados no solo. Quanto trabalho os construtores tiveram para colocar os blocos na posição durante a construção do monumento todo? Observação: A energia potencial gravitacional de um sistema corpo-Terra é definida por , em que é a massa total do corpo e é a elevação de seu centro de massa acima do nível de referência escolhido.

A equação do lado inclinado do monumento é

Onde x varia de Portanto:

O volume é:

A massa contida em um elemento de volume é :

Por causa de simetria, temos:

Onde usamos