Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 2
Um dipolo elétrico é um par de cargas iguais e opostas, e , separadas por uma distância . O momento de dipolo elétrico associado ao dipolo é o vetor , onde e aponta de para (figura). Considere um dipolo elétrico situado num campo elétrico uniforme.
a) Mostre que a resultante das forças elétricas aplicadas ao dipolo é nula, mas que o torque resultante é dado por (em relação a qualquer ponto).
b) Mostre que a energia potencial do dipolo no campo (Seç. 7.5) é dada por . Identifique as situações de equilíbrio estável e instável do dipolo no campo.
Passo 1
Para resolver o item (a), você deve lembrar algo do ensino médio: uma carga sob ação de um campo elétrico sofre uma uma força dada por
Se a carga é positiva, a força terá o mesmo sentido do campo. Se ela for negativa, terá sentido contrário. A seguir desenhamos a situação considerando a força que atua sobre e a força que atua sobre :
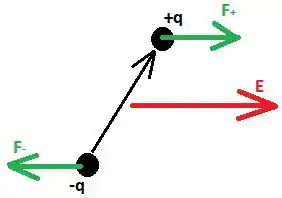
Note que a força resultante é nula:
Esse sistema consiste num binário (ver figura 11.30 do livro): um par de forças iguais e contrárias aplicadas em pontos diferentes com linhas de ação diferentes. Nesse tipo de sistema, a força resultante é sempre nula, mas o torque não é!
Passo 2
O enunciado disse para provar que o torque com relação a qualquer ponto é . Para isso, vamos tomar como referência um ponto genérico cuja posição é . As posições das cargas e são, respectivamente, e . O torque com relação ao ponto é dado por
Note que é a posição da carga (onde age a força) com relação ao ponto . O mesmo vale para . Lembre-se que na expressão do torque, temos que usar a posição onde age a força relativa ao ponto de referência que escolhemos!
Substituindo e , obtemos
Note que com isso, temos que
Observe que o termo é cancelado, sobrando
Já provamos aqui que esse torque não depende do ponto , pois o vetor sumiu. Assim, podemos escrever simplesmente:
Essa expressão é válida para qualquer ponto. Por fim, observe que
O vetor liga a carga a carga . Assim,
Bom, mas como , provamos que
Passo 3
Agora vamos para o item (b). Para calcular a energia potencial, fazemos integrais do tipo
Então de resolver o problema, vou fazer uma pequena digressão: para deslocamentos infinitesimais que podem ser intereprtados como uma rotação, temos que
Assim,
Esse é o conhecido produto misto, que satisfaz a propriedade
Assim,
Mas como , temos que
Por fim, como o produto escalar naõ depende da ordem:
Assim,
Passo 4
No nosso problema, é o ângulo que o campo forma com o dipolo. Vimos no item (a) que
Assim,
Além disso, o torque está na direção (apontando para dentro da tela), enquanto o vetor está na direção (para fora da tela), já que é perpendicular ao plano de rotação. Assim, temos que
A energia potencial é dada normalmente por
Nesse caso, ela será uma função de e pode ser adaptada para
Fazendo a integral, obtemos
Vamos definir que para , . Isso significa que a energia potencial é nula quando o dipolo é perpendicular ao campo. Essa convenção é arbitrária e só define o nível zero de energia. Com isso, achamos que
Isso pode ser escrito como
A energia será máxima para e forem antiparalelos, pois nesse caso e será mínimo se eles forem paralelos, pois assim, . No primeiro, temos uma situação de equilíbrio instável, enquanto no segundo ele é estável.
Resposta
Demonstração.