Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 14

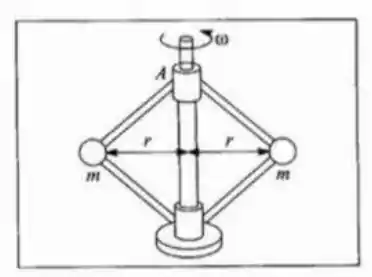
No sistema da figura, análogo a um regulador centrífugo, o anel A, de massa desprezível, pode deslizar ao longo do eixo vertical. Inicialmente, as duas bolas iguais de massa m = 200 g estão a uma distância r = 15 c m do eixo e o sistema gira com velocidade angular ω = 6 r a d s . Pressiona-se para baixo o anel A, até que a distância das bolas ao eixo aumenta para r = 25 c m . (a) Qual é a nova velocidade angular de rotação? (b) Qual é o trabalho realizado sobre o sistema?

Passo 1

Nessa aqui depois que a gente entende o que tá acontecendo fica moleza! Quando o pino de cima abaixar, por causa da rotação, os braços, que tem tamanho constante, vão ficar mais “esticados”, aumentando o raio. Assim, ó:

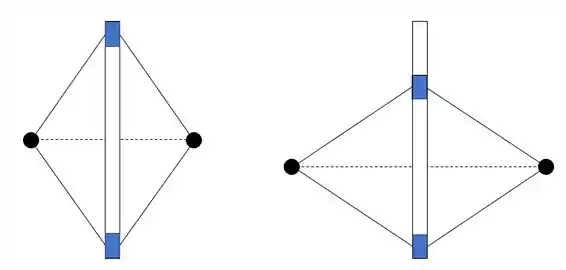
Agora que tá tudo entendido, vamos pras contas!

Passo 2

O momento angular se conserva, já que não tem nenhuma força externa!

L i = L f

I i ω i = I f ω f

As partículas a gente considera como pontuais.

m r i 2 ω i = m r f 2 ω f

Daqui,

ω f = r i r f 2 ω i

Substituindo valores:

ω f = 0.15 0.25 2 ⋅ 6

ω f = 2.16 r a d s

Passo 3

Agora vamos calcular a variação na energia, que é só rotacional!

W = Δ E r o t

W = 2 I f ω f 2 2 - 2 I i ω i 2 2

Como consideramos as massas pontuais:

W = m r f 2 ω f 2 - m r i 2 ω i 2

Substituindo valores:

W = 0.2 0.25 2 ⋅ 2.16 2 - 0.15 2 ⋅ 6 2

W = - 0.104 J

Resposta

  1. ω f = 2.16 r a d s
  2. 1.04 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está sentado em um banco giratório de piano com seus braços dobrados. (a) Quando você estende seus braços, o que acontece com a energia cinética? Qual é a razão dessa mudança? (b) Explique o que
Você está de pé sobre uma plataforma sem atrito que está girando com uma rapidez angular de 1,5r e v / s . Seus braços estão esticados para fora, e você segura um peso em cada mão. O momento de inérci
Um projétil (massa M ) é lançado a um ângulo θ , com uma rapidez inicial v 0 . Considerando o torque e momento angular em relação ao ponto de lançamento, mostre explicitamente que d L / d t = τ . Igno
Uma massa pontual de 0,20k g se movendo em uma superfície horizontal sem atrito está preso a uma tira elástica que tem a outra extremidade fixa no ponto P . A tira elástica exerce uma força de magnitu
A figura mostra um cilindro oco de 1,80 m de comprimento e 0,80 k g de massa, com raio igual a 0,20 m . O cilindro pode girar em torno de um eixo vertical que passa perpendicularmente pelo seu centro.