Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 12
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa e é puxado lentamente para cima até que o ângulo passa a . (a) Que comprimento do fio foi puxado? (b) De que fator variou a velocidade de rotação?
Passo 1
Vamos analisar a rotação dessa bolinha!
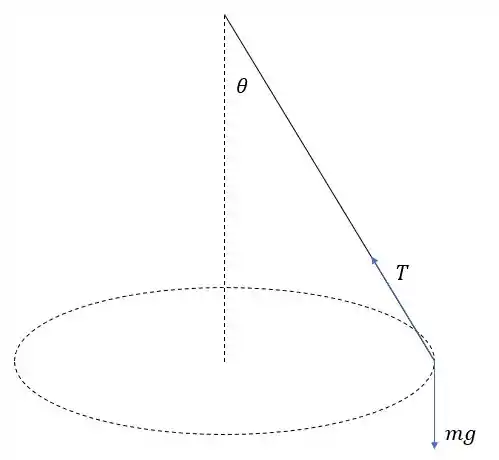
Da situação, podemos escrever:
Dividindo as duas:
No primeiro instante, o ângulo era , e depois que a corda é puxada passa a ser .
Dividindo as duas:
Passo 2
Agora vamos conservar o momento angular!
O momento de inercia de um ponto a gente já conhece!
Elevando ao quadrado:
Substituindo isso na equação do passo :
Daqui, como :
Passo 3
O fio puxado pode ser medido pela segunda situação:
Como :
E achando a razão entre as velocidades de rotação: