Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 72
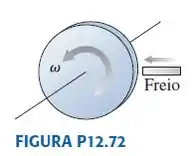
O disco de 2,0 kg e 30 cm de diâmetro da FIGURA P12.72 gira a 300 rpm. Que valor de força de atrito deve o freio exercer na borda do disco a fim de pará-lo em 30 s?
Passo 1
O disco é um corpo giratório rígido.
Vamos consultar a Figura do enunciado:
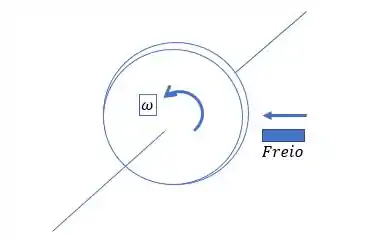
A velocidade angular inicial é de ou .
Após , o disco para.
Passo 2
Usando a equação cinemática para velocidade angular,
Implica que é:
Passo 3
Assim, o torque devido à força de atrito que deixa o disco em repouso é
Isolando :
O sinal de menos com indica que o torque devido ao atrito atua no sentido horário.
Resposta
Exercícios de Livros Relacionados
Uma escada uniforme de 2,0m e massa de 9,0k g está recostada em uma parede vertical formando um ângulo de 53,0 ° em relação ao solo. Um operário empurra a escada contra a parede, deixando-a na posição
Energia da Lua? Suponha que em algum momento no futuro você decida explorar a energia rotacional da Lua para uso na Terra. Além dos dados de astronomia no Apêndice F, você pode necessitar saber que a
Uma polia sem atrito possui o formato de um disco maciço e uniforme com massa de 2,50k g e raio de 20,0c m . Uma pedra de 1,50k g é presa a um cabo muito leve que envolve a borda da polia (Figura 9.32
Uma corda leve e flexível é enrolada diversas vezes em torno da periferia de uma casca cilíndrica com raio de 0,25m e massa igual a 40,0N , que gira sem atrito em torno de um eixo horizontal fixo. O c
Uma roda cilíndrica homogênea de raio R e massa M , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade v , e sobe sobre um plano inclinado de inclinação θ , continuando a rolar