Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 69

Volantes são grandes rodas maciças usadas para armazenar energia. Elas podem ser postas a girar lentamente, e depois a energia da roda pode ser liberada rapidamente para a realização de uma tarefa que demande alta potência. Um volante industrial com 1,5 m de diâmetro possui massa de 250   k g . Sua velocidade angular máxima é de 1.200   r p m .

a. Um motor faz o volante girar exercendo sobre ele um torque constante de 50   N   m . Quanto tempo decorre até que o volante atinja a velocidade máxima?

b. Que valor de energia estará, então, armazenada no volante?

c. O volante é desconectado do motor e conectado a uma máquina à qual deve fornecer energia. Metade da energia armazenada no volante é fornecida em 2,0   s . Qual é a potência média fornecida à máquina?

d. Que valor de torque o volante exerce sobre a máquina?

Passo 1

O volante é um corpo rígido que gira em torno de seu eixo central.

Vamos visualizar melhor:

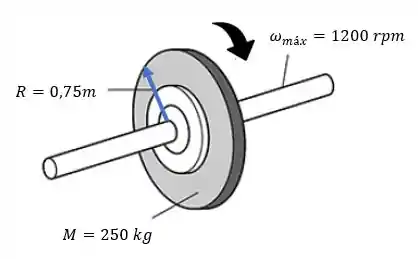
Passo 2

  1. O raio do volante é R = 0,75   m e sua massa é M = 250   k g . O momento de inércia sobre o eixo de rotação é o de um disco:

    2. I = 1 2 M R 2

    Isso implica que o momento de inercia é então:

    I = 1 2 250   k g ⋅ 0,75   m 2 = 70,31   k g ⋅ m 2

    A aceleração angular é calculada da seguinte forma:

    τ t o t a l = I α

    Isolando α :

    ⇒ α = τ t o t a l I = 50   N ⋅ m 70,31   k g ⋅ m 2 = 0,711   r a d / s 2

    O uso da equação cinemática para velocidade angular fornece:

    ω 1 = ω 0 + α t 1 - t 0

    ⇒ ω 1 = 1200   r p m = 40   π   r a d / s = 0   r a d / s + 0,711   r a d / s 2 ( t 1 - 0 s )

    Isolando t 1 :

    t 1 = 177   s

    Passo 3

  2. A energia armazenada no volante é energia cinética rotacional:

    3. K r o t = 1 2 I ω 1 2

    ⇒ K r o t = 1 2 70,31   k g ⋅ m 2 40 π ⋅ r a d / s 2 = 5,55 × 10 5 J

    A energia armazenada é de 5,6   ×   105   J .

    Passo 4

  3. Agora para descobrir a potência média fornecida à máquina fazemos:

    4. P o t ê n c i a   m é d i a   f o r n e c i d a = e n e r g i a   f o r n e c i d a i n t e r v a l o   d e   t e m p o

    Isso implica que:

    P o t ê n c i a   m é d i a   f o r n e c i d a = 5,55 × 10 5 J 2   s = 1,39 × 10 5   W = 139   k W

    Passo 5

  4. E para encontrarmos o valor de torque o volante exerce sobre a máquina fazemos:

τ = I α

⇒ τ = I ∆ ω ∆ t = I ω e n e r g i a   t o t a l - ω m e i a   e n e r g i a ∆ t .

Da parte (a) sabemos que:

ω e n e r g i a   t o t a l = ω 1 = 40 π   r a d / s

ω m e i a   e n e r g i a   pode ser obtido como:

1 2 I ω m e i a   e n e r g i a 2 = 1 2 K r o t

ω m e i a   e n e r g i a = K r o t I

Substituindo por números que já conhecemos, temos que:

ω m e i a   e n e r g i a = 5,55 × 10 5 J 70,31   k g ⋅ m 2 = 88,85   r a d / s

Passo 3

Agora podemos voltar a equação:

τ = I ω e n e r g i a   t o t a l - ω m e i a   e n e r g i a ∆ t

E substituir os valores, ficamos com:

τ = 70,31   k g ⋅ m 2 40   π   r a d / s - 88,85   r a d / s 2   s = 1,30   k N ⋅ m

Resposta

  1. t 1 = 177   s
  2. 5,6   ×   105   J
  3. 139   k W
  4. 1,30   k N ⋅ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você amarra um fio fino a um ponto na periferia de um disco uniforme vertical de raio R e massa M. O disco pode girar livremente sem atrito em um eixo horizontal fixo que passa peloseu centro de massa
Uma barra fina de comprimento l repousa sobre o eixo + O x com sua extremidade direita na origem. Um fio puxa a barra com uma força F → dirigida a um ponto P situado a uma distância h acima da barra.
Uma roda de bicicleta experimental está sob teste, montada em um eixo de modo que ela possa girar livremente em torno desse seu eixo. Se um torque de 5,0N × m for aplicado ao pneu durante 2,0 s, a vel
Um esmeril de 55,0k g é um disco sólido de diâmetro igual a 0,520m . Você comprime um machado sobre a periferia com uma força normal de 160N (Figura 10.43). O coeficiente de atrito cinético entre a lâ
Quando explora um castelo, Exena, a Exterminadora, é surpreendida por um dragão que a persegue pelo corredor. Exena corre para dentro de um quarto e tenta fechar uma porta pesada antes que o dragão en