Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 74

Uma esfera oca está rolando sobre um piso horizontal a 5,0 m/s quando chega à base de uma rampa com 30 ° de inclinação. Que distância ela percorrerá rolando na rampa antes de inverter seu movimento?

Passo 1

Suponha que a esfera oca seja um corpo rígido e que a esfera role a inclinação sem escorregar. Também assumimos que o coeficiente de atrito do rolamento é zero.

Vamos visualizar:

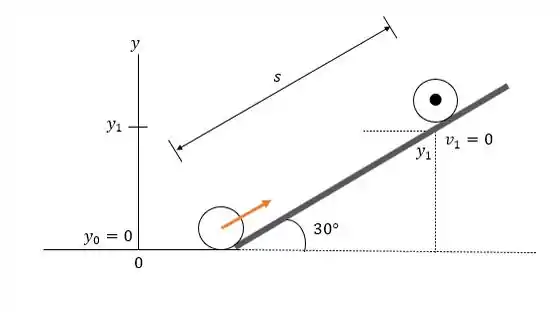
A energia cinética inicial, que é uma combinação de energia rotacional e translacional, é transformada em energia potencial gravitacional. Escolhemos o fundo da inclinação como o zero da energia potencial gravitacional.

Passo 2

A equação de conservação de energia

K f + U g f = K i + U g i é

1 2 M v 1 c m 2 + 1 2 I c m ω 1 2 + M g y 1 = 1 2 M v 0 c m 2 + 1 2 I c m ω 0 2 + M g y 0

⇒ 0   J + 0   J + M g y 1 = 1 2 M v 0 c m 2 + 1 2 2 3 M R 2 ω 0 c m 2 + 0   J

⇒ M g y 1 = 1 2 M v 0 c m 2 + 1 3 M R 2 v 0 c m 2 R 2

⇒ g y 1 = 5 6 v 0 c m 2

⇒ y 1 = 5 6 v 0 c m 2 g = 5 6 5   m / s 2 9,8   m / s 2 = 2,126   m

Passo 3

A distância percorrida ao longo da inclinação é

s = y 1 s e n   30 ° = 2,126   m 0,5 = 4,3   m

Esta é uma distância de parada razoável para um objeto rolando uma inclinação quando a velocidade na parte inferior da inclinação é de aproximadamente 10 mph.

Resposta

s = 4,3   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra fina de 0,75 m de comprimento e uma massa de 0,42 kg está suspensa por uma das extremidades. A barra é puxada para o lado e liberada para oscilar como um pêndulo, passando pela posição mais
O prato de um toca-discos tem uma velocidade angular de 8,0r a d / s no instante em que o aparelho é desligado. Três segundos depois o prato tem uma velocidade angular de 2,6r a d / s . De quantos rad
Um volante que gira em torno do eixo central está perdendo velocidade por causa do atrito com o eixo. Após o primeiro minuto de desaceleração sua velocidade angular é 0,900 vez a velocidade angular in
Um disco de vinil gira a 331 / 3 r e v / m i n no prato de um toca-discos. (a) Qual é a sua velocidade angular em radianos por segundo? Qual é a velocidade linear em um ponto do disco (b) a 15c m e (c
A figura mostra um satélite de comunicações, que é um cilindro maciço de 1210k g com 1,21m de diâmetro e 1,75m de comprimento. Antes do lançamento a parti do compartimento de carga do ônibus espacial,