Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.4 - Ex. 40
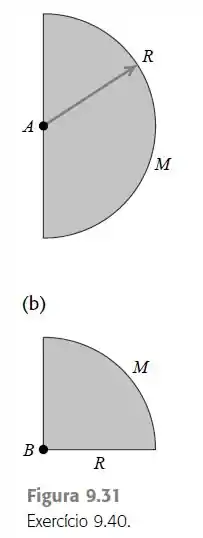
Um disco uniforme de raio é cortado ao meio, de modo que uma das metades possui massa (Figura 9.31a). a) Qual é o momento de inércia dessa metade em relação a um eixo perpendicular ao seu plano e que passa pelo ponto ? b) Por que a resposta ao item (a) é a mesma que no caso de um disco completo de massa ? c) Qual seria o momento de inércia de
um quarto de disco com massa e raio em relação a um eixo perpendicular ao seu plano e que passa pelo ponto (Figura )?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o momento de inércia do sistema em relação a um eixo para diferentes configurações.
Nós sabemos que o momento de inércia de um corpo de massa que está a uma distância do eixo de rotação é dado por:
Vamos comparar este objeto com um disco uniforme de raio e massa .
Com um eixo perpendicular à face redonda do objeto em seu centro, para um disco uniforme é o mesmo como para um cilindro sólido.
Agora que entendemos o que está acontencedo vamos aplicar a equação para o calculo do momento de inércia em cada situação!
Passo 2
a) O total de para um disco de massa e raio , será dado por:
Cada metade do disco possui o mesmo , então para o meio disco, temos:
Passo 3
b) A resposta ao item (a) é a mesma que no caso de um disco completo de massa , porque a mesma massa é distribuída da mesma maneira que uma função da distância do eixo.
Passo 4
c) O mesmo método do item (a) diz que para um quarto de disco de raio e massa é metade da metade de um disco de raio e massa , então:
Isso acontece porque depende de como a massa do objeto é distribuída em relação ao eixo, e isso é o mesmo para qualquer segmento de um disco.
Valeu, galera! Até a próxima! 😉
Resposta
- A mesma massa é distribuída da mesma maneira que uma função da distância do eixo.