Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 7

7 . || Um disco voador manobrando com aceleração constante é observado com as posições e velocidades mostradas na   F I G U R A   E X 4.7 . Qual é a aceleração a → do disco voador?

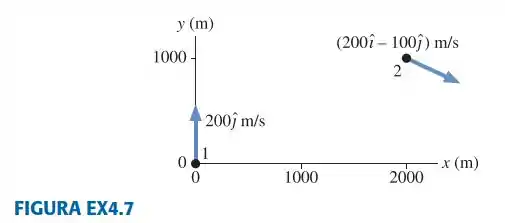
Passo 1

Nós primeiro vamos identificar os dados de cada ponto, veja que a aceleração é constante, então não está havendo variação de velocidade.

Em cada ponto nós podemos decompor cada vetor em x   e   y , veja:

x 1 = 0   m                                             y 1   =   0   m  

x 2   =   2000   m                                         y 2   =   1000   m  

v 1 x   =   0   m / s                                         v 1 y = 200   m / s  

v 2 x   =   200   m / s                                     v 2 y   = - 100   m / s

Passo 2

Com esses dados, nós podemos usar Torricelli:

v 2 2 = v 1 2 + 2 a Δ s

⇒ v 2 2 - v 1 2 2 Δ s = a

Então temos para cada componente:

a x = v 2 2 - v 1 2 2 Δ s = 200 2 - 0 2 2 ( 200 - 0 ) = 10 m / s 2

a y = v 2 2 - v 1 2 2 Δ s = - 1 00 2 - 200 2 2 ( 10 00 - 0 ) = - 15 m / s 2

Então nós podemos escrever na forma vetorial:

a → = 10 i ^ - 15 j m / s 2

Terminamos aí.

Mas se vc quiser saber o tempo vc pode fazer:

Δ t = Δ v Δ a = v 2 x - v 1 x   a i ^     = 200 - 0 10 = 10 s

Ou

Δ t = Δ v Δ a = v 2 y - v 1 y   a j ^     = - 100 - 200 - 15 = 10 s

Resposta

a → = 10 i ^ - 15 j m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um urso, acordando durante sua hibernação, sai cambaleando siretamente para nordeste ao longo de 12 m, e, depois, para leste, por mais 12 m. Mostre graficamente cada um destes deslocamentos e determin
Uma partícula tem uma aceleração constante a → = 6,0 m s 2 i ^ + 4,0 m s 2 j ^ . No tempo t=0, a velocidade é zero e o vetor posição é r → 0 = 10m i ^ . (a) Encontre os vetores velocidade e posição em
Partindo do repouso no ponto A, você dirige sua moto até o ponto B, ao norte, distante 75,0 m, aumentando a rapidez a uma taxa constante de 2,00 m/s². Então você vai gradualmente virando para o leste
O avião A está voando para o leste com uma rapidez em relação ao ar de 400 mph. Diretamente abaixo, a uma distância de 4000 ft, o avião B está apontado para o norte, voando com uma rapidez em relação
Uma partícula se move no plano xy com aceleração constante.Em t = 0 , a partícula está em r → 1 = 4,0mi ^ + 3,0m j ^ , com a velocidade v → 1 . Em t = 2,0s , a partícula está em r → 2 = 10mi ^ - 2,0m