Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 13
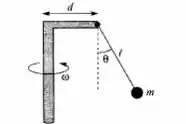
O dispositivo da figura gira em torno do eixo vertical com velocidade angular . a) Qual deve ser o valor de para que o fio de comprimento com a bolinha suspensa de massa faça um ângulo com a vertical? b) Qual é a tensão T no fio nessa situação?
Passo 1
Vamos entender o que tá rolando aqui galera, se o sistema tá girando, incluindo a bolinha óbvio, então existe uma força resultante centrípeta decorrente do giro . Desse jeito, existe um específico para que a bolinha atinga o equilíbrio quando se fala de ângulo. De boa?
Nosso diagrama fica assim
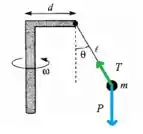
A partir disso temos
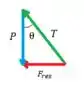
Show! Bora resolver?
Passo 2
- Já podemos ver que
- Além disso galera, nossa resultante é centrípeta, por isso
- Como queremos a relação entre vamos relacionar ambos mudando a velocidade
Vamos prestar atenção, pois aqui o raio não é dado do nosso problema, se observarmos o desenho novamente a distância da bolinha até o eixo de rotação é dada por d + o cateto oposto daquele triângulo formado por , tranquilo? Como temos a hipotenusa , fica assim