Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 3
Uma esfera uniforme de massa e raio é mantida em repouso por uma corda de massa desprezível, presa a uma parede sem atrito a uma distancia acima do centro da esfera. Determine a) a tensão na corda e b) a força que a parede exerce sobre a esfera.
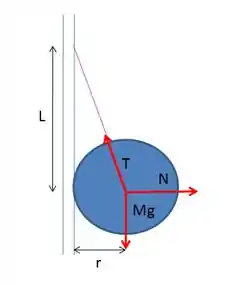
Passo 1
(a)Show de bolinhas galera, como a esfera está em equilíbrio em relação ao sistema, vamos precisar usar as equações de equilíbrio em cada eixo. Nesse caso, as forças são as que estão representadas no diagrama abaixo:
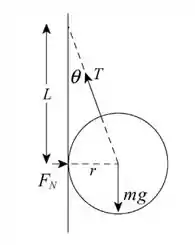
Em que , e representam a tensão na corda, a força normal exercida pela parede sobre a esfera e sua força peso, respectivamente. Sabendo disso, bora lá ver como que fica essa brincadeira toda ai.
Passo 2
Do equilíbrio vertical, obtemos que:
Tal que:
Além disso, de acordo com a figura, obtemos a relação:
Sendo assim, teremos que a tensão será dada como:
Subsituindo os valores que o enunciado nos fornece, descobrimos que a tensão vale:
Passo 3
Iradoso, agora na letra (b), temos que o equilíbrio horizontal nos fornece a relação:
E agora, como temos que:
De forma que:
E substituindo pelos valores que o enunciado nos fornece, vamos obter que:
Resposta
(a)
(b)