Uma corda de massa desprezivel está esticada horizontalmente entre dois suportes separados por uma distancia de . Quando um objeto pesando é pendurado no centro da corda, ela cede . Qual é a tensão da corda?
Passo 1
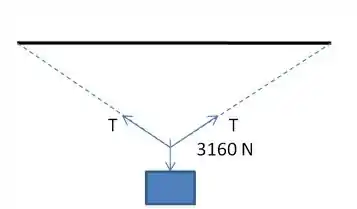
Belejóia galerinha, vamos imaginar quais são as forças que atuam no objeto azul: temos as forças com que os dois lados da corda o puxam e a força peso, como na figura a seguir.
Passo 2
Um dos passos necessários agora é relacionar as forças que atuam sobre o bloco, sabendo que ele está em equilíbrio. Lembre-se que quando forças aplicadas em diferentes direções equilibram um sistema, elas formam um triângulo. No exemplo do equilíbrio acima, temos:
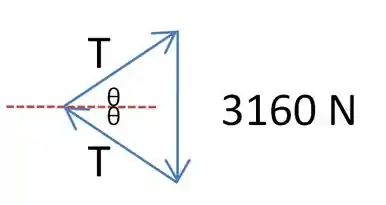
Na vertical, o bloco está em equilíbrio (assim como na horizontal). Então, chamando de o ângulo que as tensões da corda fazem com a horizontal, temos:
A questão pede a tensão na corda. Para encontrá-la vamos precisar do valor de .

Passo 3
Então, como encontrar ? Os comprimentos dados no enunciados não foram em vão! Eles servem justamente para acharmos o valor de que nos permite encontrar na relação acima. Como as tensões atuam no mesmo sentido das duas metades da corda, o ângulo que elas formam com a horizontal é o mesmo
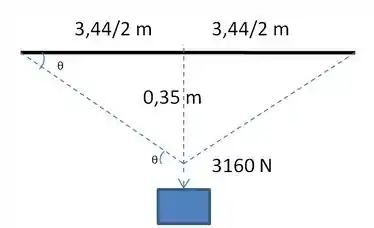
Observe a figura acima. Com base nela, podemos encontrar:
Então,
Passo 4
Pra terminar, é só substituirmos o valor de acima em . Fazendo isso, temos: