Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 82

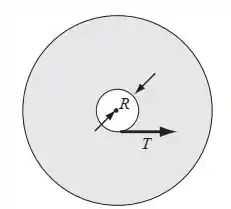
Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em torno de um eixo vertical sem atrito. O fio que está enrolado em torno do tambor passa por uma polia sem atrito e sem massa, e se prende a um bloco de massa M . O bloco é largado do repouso e o tempo t 1 que ele leva para cair a distância D é medido. O sistema é, então, reposto na configuração inicial e o objeto cujo momento de inércia I se quer determinar é colocado sobre a plataforma e o sistema é, novamente, largado do repouso. O tempo t 2 que o bloco leva para cair a mesma distância D permite, então, que se calcule I . Usando R = 10 c m , M = 2,5 k g , D = 1,8 m , t 1 = 4,2 s e t 2 = 6,8 s , (a) determine o momento de inércia da combinação plataforma-tambor. (b) Determine o momento de inércia da combinação plataforma-tambor-objeto. (c) Use seus resultados das partes (a) e (b) para determinar o momento de inércia do objeto.

Passo 1

Vamos lá. Aqui a gente vai pensar na dinâmica da translação e da rotação, para podermos achar o momento de inércia em função da aceleração. Aqui eu fiz a vista superior da situação pra ficar mais fácil de a gente entender.

Vista superior da plataforma:

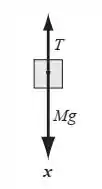
Vista lateral do objeto caindo:

Passo 2

  1. Aplicando a segunda lei de Newton para a plataforma:

    2. ∑ τ = T R = I 0 α

    Mas a gente sabe da rotação que a = α R , então:

    T R = I 0 a R

    T = I 0 a R 2

    Agora vamos olhar para o bloco:

    M g - T = M a

    T = M g - M a = M g - a

    Substituindo ali em cima:

    M g - a = I 0 a R 2

    I 0 = M g - a R 2 a

    I 0 = M R 2 g a - 1

    Passo 3

    O bloco parte do repouso e vai acelerando, até percorrer uma distância D , né? Vamos escrever a equação para o movimento do bloco, então:

    D = a t 2 2 → a = 2 D t 2

    Substituindo na expressão do momento de inércia:

    I 0 = M R 2 g 2 D t 2 - 1

    I 0 = M R 2 g t 2 2 D - 1

    Trocando pelos valores numéricos:

    I 0 = 2.5 k g × 0.10 m 2 9.81 m s 2 × 4.2 s 2 2 × 1.8 m - 1

    I 0 = 1.177   k g ⋅ m 2

    I 0 ≅ 1.2   k g ⋅ m 2

    Passo 4

  2. O momento de inércia total é igual à soma dos momentos de inércia da plataforma com o momento de inércia do objeto. O momento de inércia total é:

    3. I t o t a l = M R 2 g a - 1 = M R 2 g t 2 2 D - 1

    I t o t a l = 2.5 k g × 0.10 m 2 9.81 m s 2 × 6.8 s 2 2 × 1.8 m - 1

    I t o t a l = 3.125   k g ⋅ m 2

    Passo 5

  3. Então o momento de inércia do objeto é a diferença entre o total e o da plataforma!

I = I t o t a l - I 0

I = 3.125 - 1.177

I = 1.948   k g ⋅ m 2

Resposta

  1. I 0 = 1.177   k g ⋅ m 2
  2. I t o t a l = 3.125   k g ⋅ m 2
  3. I o b j e t o = 1.948   k g ⋅ m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois corpos estão preso a cordas que, por sua vez, estão presas a duas rodas que giram em torno do mesmo eixo, como mostrado na figura. As uas rodas estão soldadas, e modo a formarem um único objeto r
Dois corpos, de massas m 1 = 500 g e m 2 = 510 g , estão ligados por um fio de massa desprezível que passa por uma polia sem atrito. A polia é um isco uniforme de 50,0 g com um raio de 4,00 c m . O fi
O sistema da figura 9-57 é largado do repouso quando o bloco de 30 k g está 2,0 m acima da prateleira. A polia é um disco uniforme de 5,0 k g com um raio de 10 c m . Justo antes de o bloco de 30 k g a
Um cilindro uniforme de massa m 1 e raio R gira sobre suportes sem atrito. Um fio sem massa, enrolado em torno do cilindro, está ligado a um bloco de massa m 2 , que está sobre um plano inclinado de θ