Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 78

Dois corpos, de massas m 1 = 500 g e m 2 = 510 g , estão ligados por um fio de massa desprezível que passa por uma polia sem atrito. A polia é um isco uniforme de 50,0 g com um raio de 4,00 c m . O fio não desliza na polia. (a) Determine a aceleração dos corpos. (b) Qual é a tensão no fio entre o corpo de 500 g e a polia? Qual é a tensão no fio entre o corpo de 510 g e a polia? E quanto diferem estas duas tensões? (c) Qual seriam suas respostas se você desprezasse a massa da polia?

Passo 1

Bora lá, meu chegado, mais uma questãozinha de dinâmica com rotação, envolvendo polia. Nessas aí o que a gente usa? Segunda lei de Newton! Aqui embaixo eu isolei as forças, dá uma olhada.

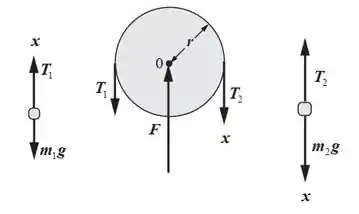
Passo 2

  1. Segunda lei de Newton para os corpos:

    2. T 1 - m 1 g = m 1 a

    m 2 g - T 2 = m 2 a

    ∑ τ = T 2 - T 1 r = I α

    Na terceira equação, I = 1 2 m p r 2 e α = a r , como sabemos da rotação.

    T 2 - T 1 r = 1 2 m p r 2 × a r

    T 2 - T 1 = 1 2 m p a

    Segura essa equação aí dentro da manga da blusa. Agora vamos somar as duas primeiras equações:

    T 1 - m 1 g + m 2 g - T 2 = m 1 + m 2 a

    T 2 - T 1 = m 2 g - m 1 g - m 1 a - m 2 a

    Agora substitui isso na equação que está guardada na manga.

    1 2 m p a = m 2 g - m 1 g - m 1 a - m 2 a

    a = m 2 - m 1 m 1 + m 2 + 1 2 m p g

    Substituindo os valores:

    a = 510 - 500 510 + 500 + 50 2 × 9.81

    a = 0.0948   m / s 2

    Passo 3

  2. Botando esse valor de aceleração na expressão das trações, vamos obter:

    3. T 1 = m 1 g + a = 0.5 9.81 + 0 . 0 948 → T 1 = 4.95 2 N

    T 2 = m 2 g - a = 0.51 9.81 - 0.0948 → T 2 = 4.9 55 N

    A diferença entre as trações é:

    Δ T = 0.0 03 N

    Passo 4

  3. Se a polia não tiver massa, a expressão da aceleração será:

a = m 2 - m 1 m 1 + m 2 g

a = 510 - 500 9.81 510 + 500

a = 0.0971   m / s 2

Substituindo na expressão das trações, vamos obter:

T 1 = 4.95 N

E

T 2 = 4.95 N

O valor é quase igual ao valor da situação com massa, pois a aceleração difere de muito pouco entre as duas situações.

Resposta

  1. a = 0.0948   m / s 2
  2. T 1 = 4.95 N , T 2 = 4.96 N , Δ T = 0.003 N
  3. T 1 = T 2 = 4.95 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema do problema 71, se a prateleira (sem atrito) for ajustada com uma inclinação, qual deve ser essa inclinação para que os blocos se movam com uma rapidez constante?
O sistema mostrado na figura consiste em um bloco de 4,0 k g colocado sobre uma prateleira horizontal sem atrito. Este bloco está preso a um cordão que passa por uma polia e tem sua outra extremida pr
Uma fita leve está enrolada em volta de um disco circular de massa m e raio r , que rola sem deslizar sobre um plano inclinado áspero de inclinação θ . A fita passa por uma roldana fixa de massa despr
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
No cilindro junto com a massa do Exemplo 9.9 (Seção 9.4), suponha que a massa m que cai seja feita de borracha, de modo que nenhuma energia mecânica é perdida quando a massa atinge o solo. a) Supondo