Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 79

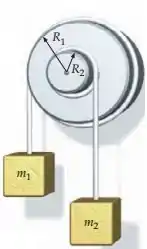
Dois corpos estão preso a cordas que, por sua vez, estão presas a duas rodas que giram em torno do mesmo eixo, como mostrado na figura. As uas rodas estão soldadas, e modo a formarem um único objeto rígido. O momento de inércia deste objeto rígido é 40 k g ⋅ m 2 . Os raios das rodas são R 1 = 1,2 m e R 2 = 0,40 m . (a) Se m 1 = 24 k g , determine m 2 de forma que não haja aceleração angular nas rodas. (b) Se 12 k g são colocados em cima de m 1 , determine a aceleração angular das rodas e as tensões nas cordas.

Passo 1

Vamos lá, meu chefe, tá entendendo tudo até agora, né? Mais uma questãozinha de dinâmica da rotação. Vamos ter que usar o que? Isso mesmo, segunda lei de Newton! Eu isolei as forças aí embaixo:

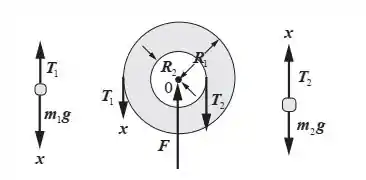
Passo 2

  1. Prestenção! Ele disse que o sistema não acelera, e se não acelera, está em equilíbrio! Mas na situação de equilíbrio, as trações são iguais aos pesos. Então, a equação para a polia vai ficar assim:

    2. ∑ τ = T 1 R 1 - T 2 R 2 = 0

    m 1 g R 1 = m 2 g R 2

    m 2 = m 1 R 1 R 2

    Substituindo valores numéricos,

    m 2 = 24 k g × 1.2 m 0.40 m

    m 2 = 72 k g

    Passo 3

  2. Beleza, agora pra situação que tem aceleração, as equações vão ficar assim ó:

m 1 g - T 1 = m 1 a 1

T 2 - m 2 g = m 2 a 2

∑ τ = T 1 R 1 - T 2 R 2 = I α

Para cada uma das polias, vamos ter a aceleração angular constante, e as acelerações tangenciais diferentes, pela equação a = α R .

m 1 g - T 1 = m 1 α R 1 → T 1 = m 1 ( g - α R 1 )

T 2 - m 2 g = m 2 α R 2 → T 2 = m 2 g + α R 2

Substituindo essas duas expressões na equação da polia:

m 1 g - α R 1 R 1 - m 2 g + α R 2 R 2 = I α

I α + m 1 R 1 2 α + m 2 R 2 2 α = m 1 g R 1 - m 2 g R 2

α = g m 1 R 1 - m 2 R 2 I + m 1 R 1 2 + m 2 R 2 2

Agora é só botar os valores numéricos:

α = 9.81 36 × 1.2 - 72 × 0.4 36 × 1.2 2 + 72 × 0.4 2 + 40

α = 1.37 r a d s 2

Por fim, a gente acha as trações!

T 1 = 36 9.81 - 1.37 × 1.2 = 0.29 k N

T 2 = 72 9.81 + 1.37 × 0.4 = 0.75 k N

Ufa, essa deu trabalho!

Resposta

  1. m 2 = 72 k g
  2. α = 1.37 r a d s 2 , T 1 = 0.29 k N e T 2 = 0.75 k N .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em 1993, um ioiô gigante de 400 k g , com 1.5 m de raio, foi largado de um guindaste de uma altura de 57 m . A corda, com uma de suas extremidades atada no topo do guindaste, ia desenrolando enquanto
A polia indicada na Figura 9.35 possui raio R e momento de inércia I. Acorda não desliza sobre a polia e esta gira em um eixo sem atrito. O coeficiente de atrito cinético entre o bloco A e o topo da m
Na Figura 9.38, o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui uma
A polia indicada na Figura 9.36 possui raio 0,160 m e momento de inércia 0,480k g ⋅ m 2 . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocida
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,