Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 15.Exercícios - Ex. 14

Uma onda em uma corda é descrita por y x , t = A c o s ( k x - ω t ) ,

  1. Faça gráficos para y ,   v y   e   a y em função de x para t = 0 .
  2. Considere os seguintes pontos sobre a corda:
  1. x = 0 ;
  2. x = π / 4 k ;
  3. x = π / 2 k ;
  4. x = 3 π / 4 k ;
  5. x = π / k ;
  6. x = 5 π / 4 k ;
  7. x = 3 π / 2 k e
  8. x = 7 π / 4 k .

Para uma partícula em cada um desses pontos para t   =   0 , descreva em palavras se a partícula está em movimento, em que sentido ela se move e diga se está aumentando de velocidade, diminuindo ou se a aceleração é instantaneamente igual a zero.

Passo 1

E aí meus amores nessa questãozinha “Pegue o que puder, sem nada a devolver” okay?

Para resolvermos este problema vamos utilizar do nosso conhecimento sobre descrição matemática das ondas, descrito na seção 15.3 deste capitulo.

Uma função de onda descreve o seu deslocamento de uma partícula no meio em um determinado instante de tempo

  1. A função de onda é assim ó:

    2. y x , t = A cos ⁡ ( k x - ω t ) ,

    o que representa uma função periódica (mas isso já sabíamos, pois é uma onda...) e sabemos também que ela é proporcional ao cosseno.

    A velocidade transversal v y é a variação temporal da posição, então derivando y ( x , 0 ) temos:

    v y = ∂ y ∂ t = A ω   s e n ( k x - ω t )

    Aqui temos que a velocidade varia com o seno.

    E a aceleração vai ser a derivada temporal da velocidade:

    a y = ∂ v y ∂ t = - A ω 2 cos ⁡ ( k x - ω t )

    Fazendo t = 0 temos as seguintes expressões para y , v y e a y :

    y = A cos ⁡ ( k x )

    v y = A ω   s e n ( k x )

    a y = - A ω 2 cos ⁡ ( k x )

    Passo 2

    A posição e a aceleração variam com o cosseno, então a cara dos dois vai ser parecida. No entanto com o sinal trocado!

    Enquanto a posição tem máxima amplitude, a aceleração tem a menor amplitude possível.

    Já a velocidade varia com o seno, então quando a y e y são nulos, a velocidade é máxima.

    E jogando tudo isso em um gráfico só vamos ter a seguinte figura:

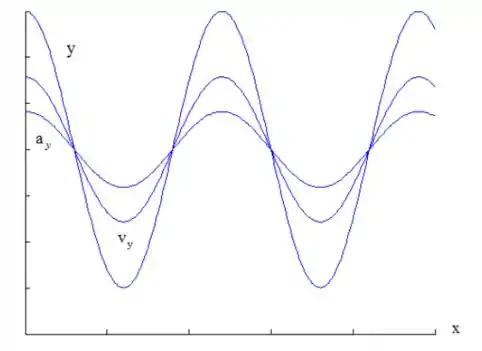
    Passo 3

  2. Agora o problema nos pede para analisar velocidade e aceleração em vários pontos da corda. Bom, do passo anterior já temos as equações que descrevem essas quantidades, certo? Essas aqui ó:

v y ( x ) = A ω   s e n ( k x )

a y ( x ) = - A ω 2 cos ⁡ ( k x )

E essas equações estão em função de x , então basta analisar cada uma delas para cada valor dado, vamos começar?

Para x = 0 :

v y 0 = A ω   s e n k x = 0

a y 0 = - A ω 2 cos ⁡ k x = - A ω 2

A partícula está instantaneamente em repouso, pois sua velocidade é zero. E ela está aumentando a velocidade, no sentido contrário do sentido positivo.

Passo 2

Para x = π / 4 k :

v y π / 4 k = A ω   s e n π / 4 = A ω 2 / 2

a y π / 4 k = - A ω 2 cos ⁡ π / 4 = - A ω 2 2 / 2

A partícula está se movimentando no sentido positivo. E ela está diminuindo a velocidade, pois velocidade e aceleração têm sinais distintos.

Passo 3

Para x = π / 2 k :

v y π / 2 k = A ω   s e n π / 2 = A ω

a y π / 2 k = - A ω 2 cos ⁡ π / 2 = 0

A partícula está se movimentando no sentido positivo com máximo valor de velocidade. E ela está momentaneamente com velocidade constante, pois a aceleração é zero.

Passo 4

Para x = 3 π / 4 k :

v y 3 π / 4 k = A ω   s e n 3 π / 4 = A ω 2 / 2

a y 3 π / 4 k = - A ω 2 cos ⁡ 3 π / 4 = A ω 2 2 / 2

A partícula está se movimentando no sentido positivo e aumentando sua velocidade, pois a aceleração tem o mesmo sinal da velocidade.

Passo 5

Para x = π / k :

v y π / k = A ω   s e n π = 0

a y π / k = - A ω 2 cos ⁡ π = A ω 2

A partícula está momentaneamente em repouso e aumentando sua velocidade.

Passo 6

Para x = 5 π / 4 k :

v y 5 π / 4 k = A ω   s e n 5 π / 4 = - A ω 2 / 2

a y 5 π / 4 k = - A ω 2 cos ⁡ 5 π / 4 = A ω 2 2 / 2

A partícula está se movimentando no sentido negativo e diminuindo sua velocidade, pois velocidade e aceleração possuem sinais opostos.

Passo 7

Para x = 3 π / 2 k :

v y 3 π / 2 k = A ω   s e n 3 π / 2 = - A ω

a y 3 π / 2 k = - A ω 2 cos ⁡ 3 π / 2 = 0

A partícula está se movimentando no sentido negativo e momentaneamente com velocidade constante, pois sua aceleração é nula

Passo 8

Para x = 7 π / 4 k :

v y 7 π / 4 k = A ω   s e n 7 π / 4 = - A ω 2 / 2

a y 7 π / 4 k = - A ω 2 cos ⁡ 7 π / 4 = - A ω 2 2 / 2

A partícula está se movimentando no sentido negativo e aumentando, pois, sua aceleração e sua velocidade possuem o mesmo sinal.

Depois dessa questão, “Ninguém se mexe” Meu cérebro caiu.”

Haha bora pra proximaaaa

Resposta

  1. Vide o passo 1 e 2
  2. Vide os passos 3 à 10.

Exercícios de Livros Relacionados

Uma onda tem uma velocidade de 240 m s e um comprimento de onda de 3,2m . Qual é (a) a frequência e (b) o período da onda?
Potência instantânea em uma onda estacionária. De acordo com a Equação (15.21), a taxa instantânea de energia transferida por uma onda ao longo de uma corda ( a potência instantânea) é dada por P x ,
Explique a razão pela qual qualquer onda descrita por uma função da forma y x , t = f ( x - v t ) se desloca no sentido +x com velocidade v .b) Mostre que y ( x , t = f - v t satisfaz à equação de ond
Velocidade de propagação da onda versus velocidade de uma partícula. (a) Mostre que a Equação 15.3 pode ser escrita na forma y x , t = A cos ⁡ 2 π λ x - v t (b) Use y ( x ,t ) para encontrar uma expre