Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 92
Duas ondas,
Propagam-se em uma corda esticada. (a) Plote a onda resultante em função de para , ,, e , onde é o comprimento de onda. Os gráficos devem se estender de até pouco mais de um período. (b) A onda resultante é a superposição de uma onda estacionária e uma onda progressiva. Em que sentido se propaga a onda progressiva? (c)Como devem ser mudadas as ondas originais para que a onda resultante seja uma superposição de uma onda estacionária e uma progressiva com as mesmas amplitudes que antes, mas com a onda progressiva se propagando no sentido oposto? Use os gráficos do item (a) para determinar o local em que a amplitude das oscilações é (d)máxima e (e)mínima. (f)Qual é a relação entre a amplitude máxima das oscilações e as amplitudes das duas ondas originais? (g)Qual é a relação entre a amplitude mínima das oscilações e as amplitudes das duas ondas originais?
Passo 1
(a)Vamos olhar para as equações das ondas apresentadas no enunciado. O número que multiplica é igual ao número de onda , que vale . Daí a gente já consegue calcular uma informação importante: . Outra coisa que a gente consegue “garimpar” do enunciado é o valor de , já que esse é o valor que multiplica nas equações das ondas. Daí, a gente tira que
Passo 2
Tá! Agora, vamos “graficar” a onda resultante da superposição de e . Como elas têm amplitudes diferentes, não vamos aqui somar as equações e transformar produto em soma. O que vamos fazer aqui é analisar os gráficos de cada uma delas nos pontos indicados e superpô-los:
1)Em : e
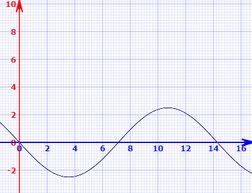
Gráfico de
Gráfico de
Superposição dos gráficos:
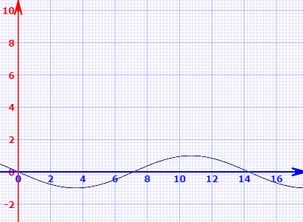
Gráfico de
2)Em : e
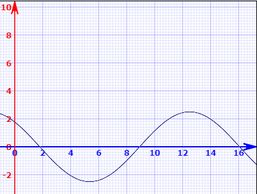
Gráfico de
Gráfico de
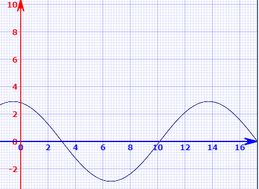
Gráfico de
3)Em : e
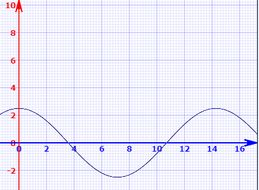
Gráfico de
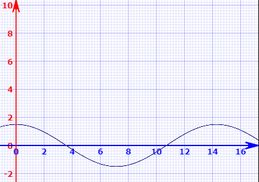
Gráfico de
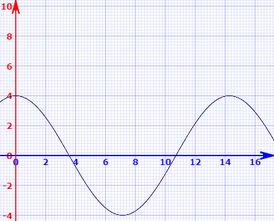
Gráfico de
4)Em : e
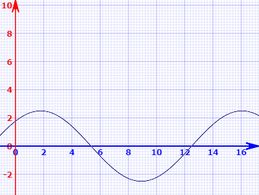
Gráfico de
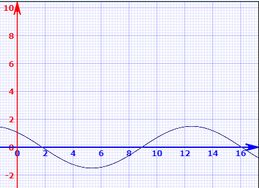
Gráfico de
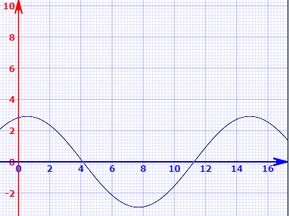
Gráfico de
5)Em : e
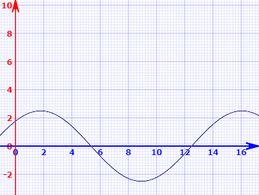
Gráfico de
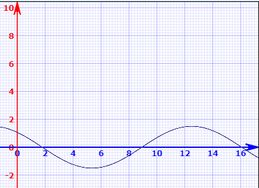
Gráfico de
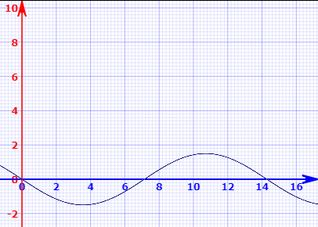
Gráfico de
Passo 3
(b) A questão nos pergunta o seguinte:
“Será que a onda resultante (obtida do somatório das duas e ) é uma onda viajante? Se sim, ela move-se em que sentido?”
Perceba que, já respondemos esse tipo de questão antes, mas, no caso, as duas ondas que se superpuseram possuíam amplitudes iguais.
E agora, José?
Não se assuste! Vamos, aqui, usar uma “malandragem” matemática:
Vamos pegar a equação de e dizer que essa onda é igual à superposição de duas outras, de amplitude e mm:
Considere, agora, que:
=
Nesse caso, temos que .
Olha aí! possuem a mesma amplitude! Vamos superpo-las então:
Repare que é uma onda estacionária e, como tal, ela não “viaja”, pois não transporta energia na direção transversal. Então, a única parcela da onda resultante responsável por esse transporte é a onda progressiva . Como essa onda possui um sinal negativo multiplicando o , podemos concluir que a onda resultante propaga-se no sentido positivo do eixo .
Passo 4
(c)Um método interessante para se conseguir ao final uma onda progressiva que se propaga no sentido oposto (sentido negativo do eixo seria alternar as amplitudes das ondas e . Note que, quando fazemos isso, a onda progressiva final será , que possui um sinal positivo na frente do e que, portanto, move-se no sentido negativo de
Passo 5
(d)Analisando os nossos gráficos do item (a), a gente consegue perceber que a maior amplitude é igual a . Ela ocorre em
Passo 6
(e)Novamente, vamos olhar para os gráficos da letra (a). Podemos ver que a menor amplitude alcançada neles é igual a . Ela é alcançada em e
Passo 7
(f)Como a onda resultante é obtida da soma das duas outras (e , podemos perceber que sua amplitude máxima é igual à soma das amplitudes máximas das outras duas:
Passo 8
(g)Semelhante ao que comentamos no passo anterior, a menor amplitude da onda resultante é igual a
Resposta
(a)
(d)
(e)
(f)
(g)