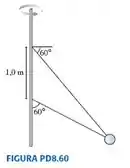
Dois arames são presos à esfera de mostrada na FIGURA . A esfera descreve um círculo horizontal com velocidade de módulo constante.

a. Para que valor de velocidade a tensão em ambos os arames é a mesma?

b. Quanto vale esta tensão?

Letra a)

Olá, tudo bem? Vou ajudar você nessa aqui! Vamos lá! Na bolinha estão agindo três forças: as duas tensões (associadas aos arames, em vermelho e em azul) e a força gravitacional (em verde), verticalmente para baixo. Note no desenho aqui embaixo que os dois arames e os pontos de fixação na haste formam um triângulo isósceles, então o comprimento é igual a .

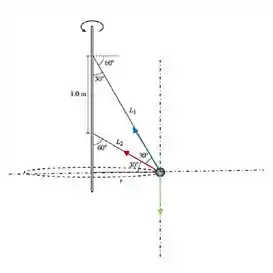
As forças na vertical são canceladas, pois o sistema não tem movimento nessa direção. Na horizontal temos que a resultante das forças é igual à força centrípeta, pois temos um movimento circular da bolinha. Usando como referência os ângulos do desenho e o eixo de coordenadas (linhas tracejadas com origem na bolinha) temos o seguinte sistema de equações:

O problema pede o valor da tensão e da velocidade para que as tensões sejam as mesmas, então podemos simplificar esse sistema fazendo :

E assim, da primeira equação temos:

E da segunda temos:

Mas sabemos que , então podemos dividir uma equação pela outra:

E ficamos com: