Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 32

Um estudante amarra uma pedra de 500   g   por um barbante de 1,0 m de comprimento e a gira sobre a cabeça em um círculo horizontal. A que valor de velocidade angular, em r p m , o barbante ficará inclinado para baixo em 10 ° ?

Passo 1

Olá, tudo bem?

Vamos listar primeiro os dados que o problema nos trás:

θ = 10 °

l = 1 m

m = 0,5 k g

E queremos saber ω .

Vou fazer um desenho pra gente ver melhor como é essa situação, saca só:

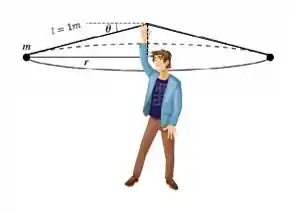
Do desenho ficou tranquilo ver que o raio da trajetória está relacionado com o ângulo de inclinação, certo? Olha como o comprimento do barbante funciona como a hipotenusa do triângulo formado com o r e com a linha pontilhada da cabeça do estudante até a mão dele. Assim temos mais um dado do problema:

r = l cos ⁡ 10 ° = 1 . cos ⁡ 10 ° = 0,985 m

Olhando com mais carinho pro desenho, temos que a tensão (que é ao longo do fio) terá duas componentes, vertical (que vai contrabalançar a gravidade) e a horizontal (que vai contrabalançar a força centrípeta). Então podemos montar o seguinte sistema:

T cos ⁡ 10 ° = m v 2 r T   s e n   10 ° = m g

Passo 2

Do sistema formado, podemos encontrar a velocidade linear v , e a partir daí encontrar ω . E é isso que vou fazer. Vamos lá?

Vou dividir a segunda equação pela primeira, assim de um lado vou ter s e n 10 ° / cos ⁡ 10 ° (a tensão vai ser cancelada) e isso equivale a t g   10 ° . Do outro vamos ter a razão de m g por m v 2 r , onde a massa pode ser cancelada, assim ó:

T   s e n   10 ° T cos ⁡ 10 ° = m g m v 2 r

t g   10 ° = g r v 2

v 2 = g r t g 10 °

v = g r t g 10 °

Agora é só substituir os valores e jogar na calculadora:

v = 9,8.0,985 t g 10 ° = 7,4 m / s

Passo 3

Beleza até aqui?

Agora com a velocidade linear podemos encontrar a velocidade angular:

v = ω r

ω = v r = 7,4 0,985 = 7,51 r a d / s

Uma última coisa: o problema pede essa velocidade em r p m , certo? Então por fim precisamos converter r a d / s para r p m , e é bem tranquilo: basta multiplicar o valor em r a d / s por 60 / 2 π :

ω = 7,51 r a d s × 60 s 1 m i n × 1 v o l t a 2 π r a d

ω = 7,51 × 60 2 π = 72 r p m

Beleza?

Espero ter ajudado!

Vamos pra próxima?

Resposta

72 r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola pesada com 100N de peso ( m = 10,2k g ) é presa ao teto de uma sala de leitura por uma corda de 4,5m de comprimento. A bola é empurrada para um lado e liberada para oscilar como um pêndulo, a
Uma bola de 100g , presa a um barbante de 60c m de comprimento, gira em um círculo vertical em torno de um ponto a 200c m do piso. Subitamente, o barbante se rompe quando está paralelo ao solo, com a
Você leva a filha pequena de seu vizinho a um parque de diversões para brincar em diversos brinquedos. Ela quer ir no brinquedo chamado O Foguete. Oito assentos em forma de foguetes são suspensos por
Um pêndulo cônico é formado por uma bola de 500g presa a um barbante de 1,0m de comprimento, fazendo com que a massa se mova em um círculo horizontal com 20c m de raio. A figura P 8.35 mostra que, ao
Dois arames são presos à esfera de 300g mostrada na FIGURA P D 8.61 . A esfera descreve um círculo horizontal com uma velocidade de módulo constante de 7,5m / s . Quanto vale a tensão em cada arame?